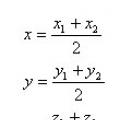- Coordenadas del punto medio del segmento.
Objetivos de la lección
- Amplíe sus horizontes de conceptos.
- Familiarícese con nuevas definiciones y recuerde algunas ya estudiadas.
- Aprenda a aplicar las propiedades de las formas al resolver problemas.
- De desarrollo: para desarrollar la atención, la perseverancia, la perseverancia, el pensamiento lógico y el habla matemática de los estudiantes.
- Educativo: a través de la lección, cultive una actitud atenta hacia los demás, inculque la capacidad de escuchar a los camaradas, la asistencia mutua y la independencia.
Objetivos de la lección
- Pon a prueba las habilidades de resolución de problemas de los estudiantes.
Plan de estudios
- Introducción.
- Repetición de material previamente estudiado.
- Coordenadas del punto medio del segmento.
- Problemas de lógica.
introducción
Antes de pasar al material sobre el tema en sí, me gustaría hablar un poco sobre un segmento no solo como una definición matemática. Muchos científicos han intentado mirar el segmento de manera diferente, vio algo inusual en él. algunos talentosos Los artistas crearon formas geométricas que transmiten estados de ánimo y emociones..
Existen muchas teorías sobre cómo el color afecta nuestro estado de ánimo y por qué.
El color se puede sentir y está estrechamente relacionado con nuestras emociones. El color de la naturaleza, la arquitectura, las plantas, la ropa que nos rodea afecta gradualmente nuestro estado de ánimo.
Según los expertos, los colores pueden afectar a una persona.
- Rojo El color puede levantarte el ánimo y darte fuerza.
- Rosa el color simboliza la paz y la tranquilidad.
- Naranja Es un color cálido e inquietante que da energía y levanta el ánimo.
- En la China Imperial amarillo Se consideraba un color tan sagrado que sólo el emperador podía vestir ropas amarillas. Los egipcios y los mayas consideraban que el amarillo era el color del sol y reverenciaban su poder para sustentar la vida. Las flores amarillas pueden vigorizar y traer alegría cuando no te sientes bien.
- Verde- color curativo. Provoca una sensación de equilibrio y armonía.
- Azul mejora la creatividad.
- Violeta- el color de la consideración, la espiritualidad y la paz. Se asocia con la intuición y el cuidado de los demás.
- Blanco Generalmente se considera el color de la pureza y la inocencia. También se asocia con la inspiración, la perspicacia, la espiritualidad y el amor.
Pero hay tanta gente y tantas opiniones. Cada uno tiene su propia verdad.
También hay una teoría interesante sobre cómo está conectado. la forma de una línea o segmento con su carácter.
La forma, como el color, es una propiedad de un objeto. Forma- estos son los contornos externos de un objeto visible, que reflejan sus aspectos espaciales (forma, traducido del latín - apariencia externa). Todo lo que nos rodea tiene una forma determinada. Comprender y representar su estructura estructural y contenido semántico es tarea del artista. Y nosotros, como espectadores, debemos poder leer la imagen, descifrar la naturaleza y el significado de sus diversas formas. En una hoja de papel y en la pantalla de una computadora, se forma una forma cuando se cierra una línea. Luego la naturaleza de la forma depende de la naturaleza de la línea por la que está formada.
¿Cuál de estas líneas puede expresar calma, enfado, indiferencia, excitación, alegría?
En este caso no puede haber una respuesta clara. Por ejemplo, una línea espinosa puede expresar ira, regodeo o alegría salvaje que raya en la imprudencia.
¿Qué estado de ánimo o emoción corresponde a cada una de estas líneas?
¿Cómo depende una forma de la naturaleza de la línea que la forma?
Repetición de material previamente estudiado.
En el espacio
Hay dos puntos arbitrarios A1(x 1 ;y 1 ;z 1) y A2(x 2 ;y 2 ;z 2). Entonces el punto medio del segmento A1A2 será el punto CON con coordenadas x, y, z, donde

Dividir un segmento en una proporción determinada
Si x 1 e y 1 son las coordenadas del punto A, y x 2 e y 2 son las coordenadas del punto B, entonces las coordenadas x e y del punto C, que dividen el segmento AB con respecto a , están determinadas por las fórmulas
El área de un triángulo según las coordenadas conocidas de sus vértices A(x 1, y 1), B(x 2, y 2), C(x 3, y 3) se calcula mediante la fórmula.
El número obtenido mediante esta fórmula debe tomarse en valor absoluto.
Ejemplo No. 1
Encuentra el punto medio del segmento AB.

Respuesta: Las coordenadas de la mitad del segmento son (1,5;2)
Ejemplo No. 2.
Encuentra el punto medio del segmento AB.
Respuesta: Las coordenadas de la mitad del segmento son iguales a (21;0)
Ejemplo No. 3.
Encuentra las coordenadas del punto C si AC=5,5 y CB=19,5.
A(1;7), B(43;-4)

Respuesta: Coordenadas del punto C(10.24;4.58)
Tareas
Tarea número 1
Encuentre el punto medio del segmento DB.

Tarea número 2.
Encuentra la mitad del segmento CD.

Cómo se hacen las estatuas.
Se dice de muchos escultores famosos que cuando se les preguntó cómo se las arreglan para hacer estatuas tan maravillosas, la respuesta fue: "Tomo un bloque de mármol y le corto todo lo innecesario". Puedes leer esto en diferentes libros sobre Miguel Ángel, sobre Thorvaldsen, sobre Rodin.


De la misma manera, puede obtener cualquier figura geométrica plana limitada: debe tomar algún cuadrado en el que se encuentre y luego cortar todo lo innecesario. Sin embargo, es necesario cortar no inmediatamente, sino gradualmente, descartando en cada paso una pieza con forma de círculo. En este caso, el círculo en sí se descarta y su borde, el círculo, permanece en la figura.
A primera vista, parece que de esta manera sólo se pueden obtener figuras de un determinado tipo. Pero la cuestión es que no descartan uno o dos círculos, sino un conjunto infinito, o más precisamente, contable de círculos. De esta forma podrás conseguir cualquier figura. Para convencerse de ello basta tener en cuenta que es contable el conjunto de círculos para los cuales tanto el radio como ambas coordenadas del centro son racionales.
Y ahora, para conseguir cualquier figura, basta con coger el cuadrado que la contiene (un bloque de mármol) y dibujar todos los círculos del tipo anterior que no contengan ni un solo punto de la figura que necesitamos. Si lanza círculos no desde un cuadrado, sino desde todo el plano, utilizando la técnica descrita podrá obtener figuras ilimitadas.
Preguntas
- ¿Qué es un segmento?
- ¿En qué consiste el segmento?
- ¿Cómo puedes encontrar el punto medio de un segmento?
Lista de fuentes utilizadas
- Kuznetsov A.V., profesor de matemáticas (grados 5 a 9), Kiev
- “Examen del Estado Unificado 2006. Matemáticas. Materiales educativos y didácticos para la preparación de estudiantes / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006"
- Mazur K. I. “Resolución de los principales problemas competitivos en matemáticas de la colección editada por M. I. Skanavi”
- L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina “Geometría, 7 – 9: libro de texto para instituciones educativas”
Trabajamos en la lección.
Kuznetsov A.V.
Poturnak S.A.
Tatiana Prosniakova
Introducción de coordenadas cartesianas en el espacio. Distancia entre puntos. Coordenadas del punto medio del segmento.
Objetivos de la lección:
Educativo: Considere el concepto de sistema de coordenadas y las coordenadas de un punto en el espacio; derivar la fórmula de la distancia en coordenadas; derivar la fórmula para las coordenadas del punto medio del segmento.
Educativo: Promover el desarrollo de la imaginación espacial de los estudiantes; Contribuir al desarrollo de la resolución de problemas y al desarrollo del pensamiento lógico de los estudiantes.
Educativo: Fomentar la actividad cognitiva, el sentido de responsabilidad, una cultura de la comunicación, una cultura del diálogo.
Equipo: Material de dibujo, presentación, centro de diseño digital.
Tipo de lección: Lección sobre cómo aprender material nuevo.
Estructura de la lección:
Organizar el tiempo.
Actualización de conocimientos básicos.
Aprender material nuevo.
Actualizando nuevos conocimientos
Resumen de la lección.
durante las clases
Mensaje de la historia " Sistema de coordenadas Cartesianas"(Aprendiz)
Al resolver un problema geométrico, físico y químico, se pueden utilizar varios sistemas de coordenadas: rectangular, polar, cilíndrico, esférico.
En el curso de educación general se estudia el sistema de coordenadas rectangulares en el plano y en el espacio. De lo contrario, se le llama sistema de coordenadas cartesiano en honor al filósofo científico francés René Descartes (1596 - 1650), quien introdujo por primera vez las coordenadas en la geometría.
(Historia de un estudiante sobre René Descartes).
René Descartes nació en 1596 en la ciudad de Lae, en el sur de Francia, en el seno de una familia noble. Mi padre quería convertir a René en oficial. Para ello, en 1613 envió a René a París. Descartes tuvo que pasar muchos años en el ejército, participando en campañas militares en Holanda, Alemania, Hungría, República Checa, Italia y en el asedio de la fortaleza hugonota de La Rochalie. Pero René estaba interesado en la filosofía, la física y las matemáticas. Poco después de su llegada a París, conoció al alumno de Vieta, un destacado matemático de la época: Mersen, y luego a otros matemáticos en Francia. Mientras estuvo en el ejército, Descartes dedicó todo su tiempo libre a las matemáticas. Estudió álgebra alemana y matemáticas francesa y griega.
Después de la captura de La Rochalie en 1628, Descartes abandonó el ejército. Lleva una vida solitaria para implementar sus amplios planes de trabajo científico.
Descartes fue el filósofo y matemático más grande de su tiempo. La obra más famosa de Descartes es su Geometría. Descartes introdujo un sistema de coordenadas que todo el mundo utiliza hoy en día. Estableció una correspondencia entre números y segmentos de recta y así introdujo el método algebraico en la geometría. Estos descubrimientos de Descartes dieron un gran impulso al desarrollo tanto de la geometría como de otras ramas de las matemáticas y la óptica. Se hizo posible representar gráficamente la dependencia de las cantidades del plano de coordenadas, los números, como segmentos, y realizar operaciones aritméticas en segmentos y otras cantidades geométricas, así como diversas funciones. Era un método completamente nuevo, que se distinguía por la belleza, la gracia y la sencillez.
Repetición. Sistema de coordenadas rectangulares en un plano.
Preguntas:
¿Qué se llama sistema de coordenadas en un plano?
¿Cómo se determinan las coordenadas de un punto en un plano?
¿Cuáles son las coordenadas del origen?
¿Cuál es la fórmula para las coordenadas del punto medio de un segmento y la distancia entre puntos en un plano?
Aprender material nuevo:
Un sistema de coordenadas rectangular en el espacio es un trío de líneas de coordenadas mutuamente perpendiculares con un origen común. El origen común se indica con la letra.oh.
Oh - eje de abscisas,
Oy – eje de ordenadas,
ACERCA DEz– aplicar eje

Tres planos que pasan por los ejes de coordenadas Ox y Oy, Oy y Oz, ACERCA DEzy Ox se llaman planos de coordenadas: Oxy, Oyz, ACERCA DEzX.
En un sistema de coordenadas rectangular, cada punto M en el espacio está asociado con un triple de números: sus coordenadas.
M(x,y,z), donde x es la abscisa, y es la ordenada,z- aplicar.
Sistema de coordenadas en el espacio.


Coordenadas de puntos

Distancia entre puntos

1 (X 1 ;y 1 ;z 1 ) y A 2 (X 2 ;y 2 ;z 2 )
Entonces la distancia entre los puntos A 1 y un 2 se calcula así:
Coordenadas del punto medio del segmento en el espacio.
Hay dos puntos arbitrarios A. 1 (X 1 ;y 1 ;z 1 ) y A 2 (X 2 ;y 2 ;z 2 ). Entonces el punto medio del segmento A 1 A 2 habrá un punto C con coordenadas x, y, z, donde

Adquirir habilidades de solución:
1) Encuentra las coordenadas de las proyecciones ortogonales de los puntos.A (1, 3, 4) y
B (5, -6, 2) a:
Un avionoxi ; b) aviónOyz ; c) ejeBuey ; d) ejeOnz .
Respuesta: a) (1, 3, 0), (5, -6, 0); b) (0, 3, 4), (0, -6, 2); c) (1, 0, 0), (5, 0, 0);
d) (0, 0, 4), (0, 0, 2).
2) ¿A qué distancia está el punto?A (1, -2, 3) desde el plano de coordenadas:
A)oxi ; b)Oxz ; V)Oyz ?
Respuesta: a) 3; segundo) 2; En 1
3) Encuentra las coordenadas de la mitad del segmento:
A)AB , SiA (1, 2, 3) yB (-1, 0, 1); b)CD , SiC (3, 3, 0) yD (3, -1, 2).
Respuesta: a) (1, 1, 2); segundo) (3, 1, 1).
5. Tarea: libro de texto de A. V. Pogorelov “Geometría 10-11” págs. 23 – 25, pág. 53 responda las preguntas nº 1 – 3; №7, №10(1)
6. Resumen de la lección.
Mesa
En la superficieEn el espacio
Definición. Un sistema de coordenadas es un conjunto de dos ejes de coordenadas que se cruzan, el punto en el que estos ejes se cruzan (el origen) y segmentos unitarios en cada uno de los ejes.
Definición. Un sistema de coordenadas es un conjunto de tres ejes de coordenadas, el punto en el que estos ejes se cruzan (el origen de las coordenadas) y segmentos unitarios en cada uno de los ejes.
2 ejes,
OU - eje de ordenadas,
OX - eje de abscisas
3 ejes,
BUEY - eje de abscisas,
OU – eje de ordenadas,
OZ - eje del aplicador.
OX es perpendicular a OA
OX es perpendicular a OU,
OX es perpendicular a OZ,
El amplificador operacional es perpendicular a OZ
(O;O)
(ooo)
Dirección, segmento único
Distancia entre puntos.
Distancia entre puntos
Coordenadas del punto medio del segmento.
Coordenadas del punto medio del segmento.
Preguntas:
¿Cómo se introduce el sistema de coordenadas cartesiano? ¿En qué consiste?
¿Cómo se determinan las coordenadas de un punto en el espacio?
¿Cuál es la coordenada del punto de intersección de los ejes coordenados?
¿Cuál es la distancia desde el origen a un punto dado?
¿Cuál es la fórmula para las coordenadas de la mitad de un segmento y la distancia entre puntos en el espacio?
Evaluación del estudiante
7.Reflexión
En la lección
Descubrí …
He aprendido…
Me gusta…
Me resultó difícil...
Mi humor…
Literatura.
AV. Pogorelov. Libro de texto 10-11. M. “Ilustración”, 2010.
ES. Petrakov. Clubes de matemáticas en los grados 8-10. M, “Ilustración”, 1987
Hay todo un grupo de tareas (incluidas en los tipos de problemas de examen) asociadas con el plano de coordenadas. Se trata de problemas que van desde los más básicos, que se resuelven de forma oral (determinación de la ordenada o abscisa de un punto determinado, o de un punto simétrico a un punto determinado, entre otros), hasta tareas que requieren conocimientos, comprensión y comprensión de gran calidad. buenas habilidades (problemas relacionados con el coeficiente angular de una línea recta).
Poco a poco los consideraremos todos. En este artículo, comenzaremos con lo básico. Son tareas sencillas de determinar: la abscisa y la ordenada de un punto, la longitud de un segmento, el punto medio de un segmento, el seno o coseno de la pendiente de una recta.La mayoría de la gente no estará interesada en estas tareas. Pero considero necesario presentarlos.
El caso es que no todo el mundo va a la escuela. Muchas personas toman el Examen Estatal Unificado 3-4 o más años después de graduarse y recuerdan vagamente qué son la abscisa y la ordenada. También analizaremos otras tareas relacionadas con el plano de coordenadas, no te lo pierdas, suscríbete a las actualizaciones del blog. Ahora norte un poco de teoría.
Construyamos el punto A en el plano coordenado con coordenadas x=6, y=3.

Dicen que la abscisa del punto A es igual a seis, la ordenada del punto A es igual a tres.
En pocas palabras, el eje buey es el eje de abscisas, el eje y es el eje de ordenadas.
Es decir, la abscisa es un punto del eje x en el que se proyecta un punto dado en el plano coordenado; La ordenada es el punto en el eje y al que se proyecta el punto especificado.
Longitud de un segmento en el plano coordenado.
Fórmula para determinar la longitud de un segmento si se conocen las coordenadas de sus extremos:

Como puedes ver, la longitud de un segmento es la longitud de la hipotenusa en un triángulo rectángulo con catetos iguales.
X B - X A y U B - U A
* * *
La mitad del segmento. Sus coordenadas.

Fórmula para encontrar las coordenadas del punto medio de un segmento:

Ecuación de una recta que pasa por dos puntos dados

La fórmula para la ecuación de una recta que pasa por dos puntos dados tiene la forma:

donde (x 1;y 1) y (x 2;y 2 ) coordenadas de puntos dados.
Sustituyendo los valores de las coordenadas en la fórmula, se reduce a la forma:
y = kx + b, donde k es la pendiente de la recta
Necesitaremos esta información para resolver otro grupo de problemas relacionados con el plano coordenado. Habrá un artículo sobre esto, ¡no te lo pierdas!
¿Qué más puedes agregar?
El ángulo de inclinación de una recta (o segmento) es el ángulo entre el eje oX y esta recta, que oscila entre 0 y 180 grados.

Consideremos las tareas.
Desde el punto (6;8) se traza una perpendicular al eje de ordenadas. Encuentra la ordenada de la base de la perpendicular.

La base de la perpendicular bajada sobre el eje de ordenadas tendrá coordenadas (0;8). La ordenada es igual a ocho.
Respuesta: 8
Encuentra la distancia desde el punto. A con coordenadas (6;8) a la ordenada.

La distancia del punto A al eje de ordenadas es igual a la abscisa del punto A.
Respuesta: 6.
A(6;8) relativo al eje Buey.

Un punto simétrico al punto A con respecto al eje oX tiene coordenadas (6; – 8).

La ordenada es igual a menos ocho.
Respuesta: – 8
Encuentra la ordenada de un punto simétrico al punto. A(6;8) relativo al origen.

Un punto simétrico al punto A con respecto al origen tiene coordenadas (– 6;– 8).
Su ordenada es –8.

Respuesta: –8
Encuentra la abscisa del punto medio del segmento que conecta los puntos.oh(0;0) y A(6;8).

Para resolver el problema, es necesario encontrar las coordenadas del medio del segmento. Las coordenadas de los extremos de nuestro segmento son (0;0) y (6;8).
Calculamos usando la fórmula:

Obtuvimos (3;4). La abscisa es igual a tres.
Respuesta: 3
*La abscisa del medio de un segmento se puede determinar sin cálculo usando una fórmula construyendo este segmento en un plano de coordenadas en una hoja de papel en un cuadrado. La mitad del segmento será fácil de determinar mediante las celdas.
Encuentra la abscisa del punto medio del segmento que conecta los puntos. A(6;8) y B(–2;2).

Para resolver el problema es necesario encontrar las coordenadas de la mitad del segmento. Las coordenadas de los extremos de nuestro segmento son (–2;2) y (6;8).
Calculamos usando la fórmula:

Obtuvimos (2;5). La abscisa es igual a dos.
Respuesta: 2
*La abscisa del medio de un segmento se puede determinar sin cálculo usando una fórmula construyendo este segmento en un plano de coordenadas en una hoja de papel en un cuadrado.
Encuentra la longitud del segmento que conecta los puntos (0;0) y (6;8).

La longitud del segmento en las coordenadas dadas de sus extremos se calcula mediante la fórmula:

en nuestro caso tenemos O(0;0) y A(6;8). Medio,
*No importa el orden de las coordenadas al restar. Puedes restar la abscisa y ordenada del punto A de la abscisa y ordenada del punto O:
Respuesta:10
Encuentra el coseno de la pendiente del segmento que conecta los puntos. oh(0;0) y A(6;8), con eje x.

El ángulo de inclinación de un segmento es el ángulo entre este segmento y el eje oX.
Desde el punto A bajamos una perpendicular al eje oX:

Es decir, el ángulo de inclinación de un segmento es el ánguloEFSen el triángulo rectángulo ABO.
El coseno de un ángulo agudo en un triángulo rectángulo es
relación entre el cateto adyacente y la hipotenusa

Necesitamos encontrar la hipotenusa.OA.
Según el teorema de Pitágoras:En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Por tanto, el coseno del ángulo de la pendiente es 0,6
Respuesta: 0,6
Desde el punto (6;8) se traza una perpendicular al eje de abscisas. Encuentra la abscisa de la base de la perpendicular.

Se traza una línea recta paralela al eje de abscisas que pasa por el punto (6;8). Encuentra la ordenada de su punto de intersección con el eje. UNED.

Encuentra la distancia desde el punto. A con coordenadas (6;8) al eje de abscisas.

Encuentra la distancia desde el punto. A con coordenadas (6;8) al origen.

Sean A(X 1; y 1) y B(x 2; y 2) dos puntos arbitrarios y C (x; y) el punto medio del segmento AB. Encontremos las coordenadas x, y del punto C.
Consideremos primero el caso en el que el segmento AB no es paralelo al eje y, es decir, X 1 X 2. Dibujemos líneas rectas que pasen por los puntos A, B, C, paralelas al eje y (Fig. 173). Intersecarán el eje x en los puntos A 1 (X 1; 0), B 1 (X 2; 0), C 1 (x; 0). Según el teorema de Tales, el punto C 1 será el punto medio del segmento A 1 B 1.

Dado que el punto C 1 es el medio del segmento AiBi, entonces A 1 C 1 = B 1 C 1, lo que significa Ix - X 1 I = Ix - X 2 I. Se deduce que x - x 1 = x - x 2 , o (x - x 1) = -(x-x 2).
La primera igualdad es imposible, ya que x 1 x 2. Luego lo segundo es cierto. Y de esto obtenemos la fórmula
Si x 1 =x 2, es decir, el segmento AB es paralelo al eje y, entonces los tres puntos A 1, B 1, C 1 tienen la misma abscisa. Esto significa que la fórmula sigue siendo válida en este caso.
La ordenada del punto C se encuentra de manera similar. Por los puntos A, B, C se trazan líneas rectas paralelas al eje x. La fórmula resulta ser
Problema (15). Dados tres vértices del paralelogramo ABCD: A (1; 0), B (2; 3), C (3; 2). Encuentra las coordenadas del cuarto vértice D y los puntos de intersección de las diagonales.
Solución. El punto de intersección de las diagonales es el punto medio de cada una de ellas. Por tanto, es el punto medio del segmento AC, lo que significa que tiene coordenadas
![]()
Ahora, conociendo las coordenadas del punto de intersección de las diagonales, encontramos las coordenadas x, y del cuarto vértice D. Utilizando el hecho de que el punto de intersección de las diagonales es el punto medio del segmento BD, tenemos:

A. V. Pogorelov, Geometría para los grados 7-11, Libro de texto para instituciones educativas
Después de un arduo trabajo, de repente me di cuenta de que el tamaño de las páginas web es bastante grande, y si las cosas continúan así, entonces puedo volverme loco tranquilamente =) Por lo tanto, les traigo un breve ensayo dedicado a un problema geométrico muy común: acerca de dividir un segmento a este respecto y, como caso especial, acerca de dividir un segmento por la mitad.
Por una razón u otra, esta tarea no encajaba en otras lecciones, pero ahora tenemos una gran oportunidad para considerarla en detalle y con tranquilidad. La buena noticia es que nos tomaremos un descanso de los vectores y nos centraremos en puntos y segmentos.
Fórmulas para dividir un segmento a este respecto.El concepto de dividir un segmento a este respecto.
El concepto de dividir un segmento a este respecto.
A menudo no es necesario esperar en absoluto a lo prometido; veamos inmediatamente un par de puntos y, obviamente, lo increíble: el segmento:
El problema considerado es válido tanto para segmentos del plano como para segmentos del espacio. Es decir, el segmento de demostración se puede colocar como se desee en un plano o en el espacio. Para facilitar la explicación, lo dibujé horizontalmente.
¿Qué vamos a hacer con este segmento? Esta vez para cortar. Alguien está recortando el presupuesto, alguien está recortando su cónyuge, alguien está cortando leña y comenzaremos a cortar el segmento en dos partes. El segmento se divide en dos partes utilizando un punto determinado, que, por supuesto, se encuentra directamente sobre él:
En este ejemplo, el punto divide el segmento de tal manera que el segmento mide la mitad de largo que el segmento. TAMBIÉN se puede decir que un punto divide a un segmento en una proporción (“uno a dos”), contando desde el vértice.
En lenguaje matemático seco, este hecho se escribe de la siguiente manera: , o más a menudo en forma de la proporción habitual: . La proporción de segmentos suele denotarse con la letra griega “lambda”, en este caso: .
Es fácil componer la proporción en un orden diferente: - esta notación significa que el segmento es dos veces más largo que el segmento, pero esto no tiene ningún significado fundamental para resolver problemas. Puede ser así o puede ser así.
Por supuesto, el segmento se puede dividir fácilmente en otros aspectos y, para reforzar el concepto, el segundo ejemplo:
Aquí es válida la siguiente relación: . Si hacemos la proporción al revés, obtenemos: .
Una vez que hayamos descubierto qué significa dividir un segmento a este respecto, pasemos a considerar problemas prácticos.
Si se conocen dos puntos del plano, entonces las coordenadas del punto que divide el segmento en relación con se expresan mediante las fórmulas: ![]()
¿De dónde vinieron estas fórmulas? En el curso de geometría analítica, estas fórmulas se derivan estrictamente utilizando vectores (¿dónde estaríamos sin ellos? =)). Además, son válidos no sólo para el sistema de coordenadas cartesiano, sino también para un sistema de coordenadas afín arbitrario (ver lección Dependencia lineal (no) de vectores. Base de vectores). Ésta es una tarea tan universal.
Ejemplo 1
Encuentre las coordenadas del punto que divide el segmento en la relación si se conocen los puntos ![]()
Solución: En este problema. Usando las fórmulas para dividir un segmento en esta relación, encontramos el punto: 
Respuesta:
Preste atención a la técnica de cálculo: primero debe calcular por separado el numerador y el denominador. El resultado es a menudo (pero no siempre) una fracción de tres o cuatro pisos. Después de esto, nos deshacemos de la estructura de varios pisos de la fracción y realizamos las simplificaciones finales.
La tarea no requiere dibujo, pero siempre es útil realizarla en forma de borrador:

De hecho, la relación se cumple, es decir, el segmento es tres veces más corto que el segmento. Si la proporción no es obvia, entonces los segmentos siempre se pueden medir estúpidamente con una regla común.
Igualmente valioso segunda solución: en él la cuenta regresiva comienza desde un punto y la siguiente relación es justa: ![]() (en palabras humanas, un segmento es tres veces más largo que un segmento). Según las fórmulas para dividir un segmento a este respecto:
(en palabras humanas, un segmento es tres veces más largo que un segmento). Según las fórmulas para dividir un segmento a este respecto: 
Respuesta:
Tenga en cuenta que en las fórmulas es necesario mover las coordenadas del punto al primer lugar, ya que con él comenzó un pequeño thriller.
También está claro que el segundo método es más racional debido a que los cálculos son más sencillos. Pero aun así, este problema a menudo se resuelve de la manera “tradicional”. Por ejemplo, si según la condición se da un segmento, entonces se supone que formarás una proporción; si se da un segmento, entonces la proporción está “tácitamente” implícita.
Y di el segundo método porque a menudo intentan confundir deliberadamente las condiciones del problema. Por eso es muy importante realizar un dibujo aproximado para, en primer lugar, analizar correctamente el estado y, en segundo lugar, a efectos de verificación. Es una pena cometer errores en una tarea tan sencilla.
Ejemplo 2
Se dan puntos ![]() . Encontrar:
. Encontrar:
a) un punto que divide el segmento en relación con ;
b) un punto que divide el segmento en relación con .
Este es un ejemplo para que lo resuelvas por tu cuenta. Solución completa y respuesta al final de la lección.
A veces hay problemas en los que se desconoce uno de los extremos del segmento:
Ejemplo 3
El punto pertenece al segmento. Se sabe que un segmento tiene el doble de largo que un segmento. Encuentra el punto si ![]() .
.
Solución: De la condición se sigue que el punto divide al segmento en la razón , contando desde el vértice, es decir, la proporción es válida: . Según las fórmulas para dividir un segmento a este respecto: ![]()
Ahora no conocemos las coordenadas del punto :, pero esto no es un problema particular, ya que se pueden expresar fácilmente a partir de las fórmulas anteriores. No cuesta nada expresarlo en términos generales, es mucho más fácil sustituir números específicos y realizar los cálculos cuidadosamente: 
Respuesta:
Para comprobarlo, puedes tomar los extremos del segmento y, usando fórmulas en orden directo, asegurarte de que la relación realmente resulte en un punto. Y, por supuesto, un dibujo no será superfluo. Y para finalmente convencerte de los beneficios de una libreta de cuadros, un simple lápiz y una regla, te propongo un problema complicado que puedes resolver por tu cuenta:
Ejemplo 4
Punto . El segmento es una vez y media más corto que el segmento. Encontrar un punto si se conocen las coordenadas de los puntos. ![]() .
.
La solución está al final de la lección. Por cierto, no es el único, si sigues un camino diferente al de la muestra no será un error, lo principal es que las respuestas coincidan.
Para los segmentos espaciales todo será exactamente igual, sólo se agregará una coordenada más.
Si se conocen dos puntos en el espacio, entonces las coordenadas del punto que divide el segmento en relación con se expresan mediante las fórmulas:
.
Ejemplo 5
Se dan puntos. Encuentre las coordenadas de un punto perteneciente al segmento si se sabe que ![]() .
.
Solución: La condición implica la relación: ![]() . Este ejemplo fue tomado de una prueba real, y su autor se permitió una pequeña broma (en caso de que alguien tropezara): habría sido más racional escribir la proporción en la condición así:
. Este ejemplo fue tomado de una prueba real, y su autor se permitió una pequeña broma (en caso de que alguien tropezara): habría sido más racional escribir la proporción en la condición así: ![]() .
.
Según las fórmulas para las coordenadas del punto medio del segmento:
Respuesta: ![]()
Los dibujos en 3D con fines de inspección son mucho más difíciles de producir. Sin embargo, siempre se puede hacer un dibujo esquemático para comprender al menos la condición: qué segmentos deben correlacionarse.
En cuanto a las fracciones en la respuesta, no te sorprendas, es algo común. Lo he dicho muchas veces, pero lo repetiré: en matemáticas superiores se acostumbra utilizar fracciones ordinarias, regulares e impropias. La respuesta está en la forma. ![]() servirá, pero la opción con fracciones impropias es más estándar.
servirá, pero la opción con fracciones impropias es más estándar.
Tarea de calentamiento para una solución independiente:
Ejemplo 6
Se dan puntos. Encuentra las coordenadas del punto si se sabe que divide el segmento en la proporción.
La solución y la respuesta están al final de la lección. Si le resulta difícil navegar por las proporciones, haga un dibujo esquemático.
En el trabajo independiente y de prueba, los ejemplos considerados se encuentran solos y como parte integral de tareas más amplias. En este sentido, el problema de encontrar el centro de gravedad de un triángulo es típico.
No veo mucho sentido en analizar el tipo de tarea donde se desconoce uno de los extremos del segmento, ya que todo será similar al caso plano, excepto que hay un poco más de cálculos. Recordemos mejor nuestros años escolares:
Fórmulas para las coordenadas del punto medio de un segmento.
Incluso los lectores inexpertos pueden recordar cómo dividir un segmento por la mitad. El problema de dividir un segmento en dos partes iguales es un caso especial de división de un segmento a este respecto. La sierra a dos manos funciona de la forma más democrática y cada vecino del escritorio recibe el mismo palo:
A esta hora solemne redoblan los tambores dando la bienvenida a la importante proporción. Y fórmulas generales ![]() milagrosamente transformado en algo familiar y simple:
milagrosamente transformado en algo familiar y simple: ![]()
Un punto conveniente es el hecho de que las coordenadas de los extremos del segmento se pueden reorganizar sin problemas: ![]()
En fórmulas generales, una habitación tan lujosa, como comprenderá, no funciona. Y aquí no hay ninguna necesidad particular, por lo que es una cosita agradable.
Para el caso espacial, se cumple una analogía obvia. Si se dan los extremos de un segmento, las coordenadas de su punto medio se expresan mediante las fórmulas:
Ejemplo 7
Un paralelogramo está definido por las coordenadas de sus vértices. Encuentra el punto de intersección de sus diagonales.
Solución: Quienes lo deseen pueden completar el dibujo. Recomiendo especialmente el graffiti a aquellos que se han olvidado por completo del curso de geometría de la escuela.
Según la conocida propiedad, las diagonales de un paralelogramo se dividen por la mitad por su punto de intersección, por lo que el problema se puede resolver de dos formas.
Método uno: Considere vértices opuestos ![]() . Usando las fórmulas para dividir un segmento por la mitad, encontramos la mitad de la diagonal:
. Usando las fórmulas para dividir un segmento por la mitad, encontramos la mitad de la diagonal: