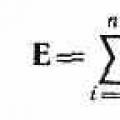Nézzünk egy módszert a feszültségvektor értékének és irányának meghatározására E az álló töltések rendszere által létrehozott elektrosztatikus tér minden pontján q 1 , q 2 , ..., K n .
A tapasztalat azt mutatja, hogy a mechanikában tárgyalt erők hatásának függetlenségének elve (lásd 6. §) alkalmazható a Coulomb-erőkre, i.e. eredő erő F, eljárva a mezőről a teszttöltésen K 0, egyenlő az erők vektorösszegével F az egyes töltések Q i oldaláról alkalmaztam:
A (79.1) szerint F=Q 0 EÉs F i ,=Q 0 Eén, hol E az eredményül kapott mező erőssége, és E i a töltés által létrehozott térerősség Kén. Az utolsó kifejezéseket (80.1) behelyettesítve kapjuk

A (80.2) képlet kifejezi az elektrosztatikus mezők szuperpozíciójának (ráhelyezésének) elve, mely feszültség szerint E a díjrendszer által létrehozott mező egyenlő azzal geometriai összeg az egyes töltések által egy adott pontban létrehozott térerősségeket külön-külön.
A szuperpozíció elve alkalmazható az elektromos dipólus elektrosztatikus mezőjének kiszámítására. Elektromos dipólus- két egyenlő modulusú ellentétes ponttöltés rendszere (+ Q, - K), távolság l amelyek között lényegesen kisebb a távolság a mező figyelembe vett pontjaitól. A dipólus tengelye (mindkét töltésen áthaladó egyenes) mentén a negatív töltéstől a pozitív töltésig irányított és a köztük lévő távolsággal egyenlő vektort ún. dipólus karl . Vektor
![]()
irányában egybeesik a dipólus karjával és egyenlő a töltés szorzatával

| K| a vállán l , hívott elektromos dipólusmomentum p vagy dipólmomentum(122. ábra).
A szuperpozíciós elv (80.2) szerint a feszültség E dipólusmezők tetszőleges pontban
E=E + + E - ,
Ahol E+ és E- - pozitív és negatív töltések által létrehozott térerősségek, ill. Ezzel a képlettel számítjuk ki a térerősséget a dipólus tengelyének kiterjedése mentén és a tengely közepére merőlegesen.
1. Térerősség a dipólus tengelye mentén azon a ponton A(123. ábra). Amint az ábrán látható, a dipólus térerőssége a pontban A a dipólus tengelye mentén irányul és egyenlő nagyságú
E A =E + -E - .
A ponttól való távolság jelölése A a dipólus tengely közepéig l-en keresztül, a (79.2) képlet alapján a vákuumra felírhatjuk

A dipólus definíciója szerint l/2< 2. Térerősség a tengelyre a közepétől megemelt merőlegesen, azon a ponton BAN BEN(123. ábra). Pont BAN BEN tehát egyenlő távolságra van a töltésektől Ahol r"
- távolság a ponttól BAN BEN a dipólus kar közepéig. Az egyenlő szárúak hasonlóságából- a megadott háromszögek közül a dipóluskar és az еv vektor alapján kapjuk E B =E +
l/
r".
(80.5) Ha a (80,4) értéket behelyettesítjük a (80,5) kifejezésbe, megkapjuk Vektor E B iránya ellentétes a dipólus elektromos nyomatékával (vektor R negatív töltésről pozitívra irányítva). Az elektrosztatika egyik feladata a térbeli töltések adott stacioner eloszlása esetén a térparaméterek felmérése. És a szuperpozíció elve az egyik lehetőség egy ilyen probléma megoldására. Tételezzük fel három egymással kölcsönhatásban lévő ponttöltés jelenlétét. Kísérlet segítségével meg lehet mérni az egyes töltésekre ható erőket. Ahhoz, hogy meghatározzuk azt a teljes erőt, amellyel két másik töltés hat egy töltésre, össze kell adni e kettő erőit a paralelogramma szabály szerint. Ebben az esetben a logikus kérdés az, hogy az egyes töltésekre ható mért erő és két másik töltésből származó erők összessége egyenlő-e egymással, ha az erőket a Coulomb-törvény szerint számítjuk? A kutatási eredmények pozitív választ mutatnak erre a kérdésre: a mért erő valóban egyenlő a Coulomb-törvény szerint más töltésekre számított erők összegével. Ezt a következtetést állítások halmazaként írják le, és szuperpozíció elvének nevezik. 1. definíció Szuperpozíció elve: A töltésmezők szuperpozíciójának elve az egyik alapja egy olyan jelenségnek, mint az elektromosságnak: jelentősége összevethető a Coulomb-törvény fontosságával. Abban az esetben, ha N töltéshalmazról (azaz több térforrásról) beszélünk, akkor a teszttöltés által kifejtett összerő q, a következő képlettel határozható meg: F → = ∑ i = 1 N F i a → , ahol F i a → az az erő, amellyel a töltésre hat q díj
q i ha nincs más N - 1 töltés. A ponttöltések közötti kölcsönhatás törvényét alkalmazva a szuperpozíció elvét alkalmazva meghatározható a véges dimenziójú testen jelenlévő töltések közötti kölcsönhatási erő. Ebből a célból minden töltést kis d q töltésekre osztunk (ponttöltéseknek fogjuk őket tekinteni), amelyeket aztán párokban veszünk; kiszámítjuk a kölcsönhatási erőt, és végül végrehajtjuk a kapott erők vektoros összeadását. Mezőértelmezés: Két ponttöltés térereje az egyes töltések által a másik hiányában létrehozott intenzitások összege. Általános esetekben a feszültségekre vonatkozó szuperpozíció elve a következő jelöléssel rendelkezik: E → = ∑ E i → , ahol E i → = 1 4 π ε 0 q i ε r i 3 r i → az i-edik ponttöltés intenzitása, r i → az i-edik töltéstől a tér egy bizonyos pontjáig húzott vektor sugara. Ez a képlet azt mondja nekünk, hogy tetszőleges számú ponttöltés térerőssége az egyes ponttöltések térerősségének összege, ha nincs más. A mérnöki gyakorlat megerősíti a szuperpozíció elvének való megfelelést még nagyon nagy térerősség esetén is. Az atomokban és az atommagokban lévő mezők erőssége jelentős (10 11 - 10 17 V m nagyságrendű), de ebben az esetben is a szuperpozíció elvét alkalmazták az energiaszintek kiszámításához. Ebben az esetben a számítások eredményei nagy pontossággal egybeestek a kísérleti adatokkal. Ugyanakkor azt is meg kell jegyezni, hogy nagyon kis távolságok (~10-15 m nagyságrendű) és rendkívül erős mezők esetén valószínűleg nem teljesül a szuperpozíció elve. 1. példa Például nehéz atommagok felületén ~ 10 22 V m nagyságrendű erősségnél teljesül a szuperpozíció elve, és 10 20 V m erősségnél a kölcsönhatás kvantummechanikai nemlinearitásai keletkeznek. Ha a töltéseloszlás folyamatos (azaz nem kell figyelembe venni a diszkrétséget), a teljes térerősséget a következő képlet adja meg: E → = ∫ d E → . Ebben a bejegyzésben az integráció a töltéselosztási régióban történik: A szuperpozíció elve lehetővé teszi, hogy egy ismert típusú térbeli töltéseloszlás esetén a tér bármely pontjára E → értéket találjunk. Azonos q ponttöltések vannak megadva, amelyek az a oldalú négyzet csúcsaiban helyezkednek el. Meg kell határozni, hogy az egyes töltésekre milyen erőt fejt ki a másik három töltés. Megoldás
Az 1. ábrán szemléltetjük a négyzet csúcsaiban az adott töltések bármelyikére ható erőket. Mivel a feltételben az szerepel, hogy a díjak azonosak, illusztrációként bármelyiket választhatjuk. Írjuk fel a q 1 töltésre ható összegző erőt: F → = F 12 → + F 14 → + F 13 → . Az F 12 → és az F 14 → erők nagysága egyenlő, a következőképpen határozzuk meg őket: F 13 → = k q 2 2 a 2 . Rajz 1 Most állítsuk be az O X tengely irányát (1. ábra), tervezzük meg az F → = F 12 → + F 14 → + F 13 → egyenletet, cseréljük be a fent kapott erőmodulokat, majd: F = 2 k q 2 a 2 · 2 2 + k q 2 2 a 2 = k q 2 a 2 2 2 + 1 2. Válasz: a négyzet csúcsaiban található adott töltések mindegyikére kifejtett erő egyenlő F = k q 2 a 2 2 2 + 1 2. 3. példa Elektromos töltést kapunk, amely egyenletesen oszlik el egy vékony szál mentén (τ lineáris sűrűséggel). Fel kell írni egy kifejezést, amely a szál végétől a távolságra határozza meg a térerősséget a folytatása mentén. Menethossz – l .
Rajz 2 Megoldás
Első lépésünk egy ponttöltés kiemelése lesz a szálon d q. Készítsünk hozzá a Coulomb-törvénynek megfelelően egy rekordot, amely kifejezi az elektrosztatikus tér erősségét: d E → = k d q r 3 r → . Egy adott pontban minden feszültségvektor azonos irányú az OX tengely mentén, akkor: d E x = k d q r 2 = d E . A probléma feltétele, hogy a töltés adott sűrűségű menet mentén egyenletes eloszlású legyen, és a következőket írjuk: Helyettesítsük be ezt a bejegyzést az elektrosztatikus térerősség korábban írt kifejezésébe, integráljuk és kapjuk: E = k ∫ a l + a τ d r r 2 = k τ - 1 r a l + a = k τ l a (l + a) . Válasz: A jelzett pontban a térerősséget az E = k τ l a (l + a) képlet határozza meg. Ha hibát észlel a szövegben, jelölje ki, és nyomja meg a Ctrl+Enter billentyűkombinációt Elektrosztatika Elektrosztatika- az elektromosság tanulmányozásának egy része, amely az álló elektromos töltések kölcsönhatását és az állandó elektromos tér tulajdonságait vizsgálja. 1.Elektromos töltés.
Az elektromos töltés az belső tulajdonság testek vagy részecskék, amelyek elektromágneses kölcsönhatásra való képességüket jellemzik. Az elektromos töltés mértékegysége a coulomb (C)- 1 másodperc alatt 1 amper áramerősséggel egy vezető keresztmetszetén áthaladó elektromos töltés. Létezik elemi (minimális) elektromos töltés
Az elemi negatív töltés hordozója az elektron
.
A tömege Az elektromos töltés kísérletileg megállapított alapvető tulajdonságai: Két típusa van: pozitív
És negatív
.
Mint a töltések taszítanak, ellentétben a töltések vonzzák. Elektromos töltés állandó- értéke nem függ a referenciarendszertől, pl. attól függően, hogy mozgásban vagy nyugalomban van. Elektromos töltés diszkrét- bármely test töltése az elemi elektromos töltés egész számú többszöröse e. Elektromos töltés adalékanyag- bármely testrendszer (részecske) töltése megegyezik a rendszerben lévő testek (részecskék) töltéseinek összegével. Az elektromos töltés engedelmeskedik díj természetvédelmi törvény
: Ebben az esetben zárt rendszer alatt olyan rendszert értünk, amely nem cserél töltést külső testekkel. Az elektrosztatika fizikai modellt használ - pont elektromos töltés- töltött test, amelynek alakja és méretei ebben a feladatban lényegtelenek. 2.Coulomb törvénye
A ponttöltések kölcsönhatásának törvénye - Coulomb törvénye: interakciós erő F két állópontos töltés között, vákuumban található, arányos a díjakkal és
fordítottan arányos a távolság négyzetével r közöttük: Kényszerítés
kölcsönható töltéseket összekötő egyenes vonal mentén irányul, azaz. központi, és megfelel a vonzásnak (F<0) в случае разноименных зарядов и отталкиванию (F> 0) azonos nevű díjak esetén. Vektor formában a töltésre ható erő: Töltésenként q 2 töltés oldala
erő hat - elektromos állandó,
az egyik alapvető fizikai állandó: Ahol farad (F)- az elektromos kapacitás mértékegysége (21. pont). Ha a kölcsönható töltések izotróp közegben vannak, akkor a Coulomb-erő Ahol - a közeg dielektromos állandója- dimenzió nélküli mennyiség, amely megmutatja, hogy a kölcsönhatási erő hányszorosa F töltések közötti egy adott közegben kisebb, mint a kölcsönhatási erejük
vákuumban: A vákuum dielektromos állandója. A dielektrikumokról és tulajdonságaikról az alábbiakban részletesebben lesz szó (15. fejezet). Bármilyen feltöltött test figyelembe vehető Hogyan totalitás pontdíjak, hasonlóan ahhoz, ahogy a mechanikában bármely test anyagi pontok gyűjteményének tekinthető. Ezért elektrosztatikus erő, amellyel az egyik töltött test a másikra hat, egyenlő geometriai erőösszeg, amelyet a második test minden ponttöltésére alkalmazunk az első test minden ponttöltésének oldaláról. Gyakran sokkal kényelmesebb azt feltételezni, hogy a díjakat töltött testben folyamatosan elosztva
- mentén néhány vonalak(például feltöltött vékony rúd esetén), felületek(például feltöltött lemez esetén) ill hangerő. Ennek megfelelően használják a fogalmakat lineáris, felületi és térfogati töltéssűrűség. Az elektromos töltések térfogatsűrűsége Ahol dq- feltöltött test kis elemének töltése térfogattal dV. Az elektromos töltések felületi sűrűsége
Ahol dq- feltöltött felület kis szakaszának töltése területtel dS. Az elektromos töltések lineáris sűrűsége Ahol dq- egy feltöltött vezetékhossz kis szakaszának töltése dl. 3.
Az elektrosztatikus mező az álló elektromos töltések által létrehozott mező. Az elektrosztatikus mezőt két mennyiség írja le: lehetséges(energia skalár mezőjellemző) és feszültség(erő vektor mezőjellemző). Elektrosztatikus térerősség- vektor a ható erő által meghatározott fizikai mennyiség egységenként pozitív a mező egy adott pontján elhelyezett töltés: Az elektrosztatikus térerősség mértékegysége newton per coulomb(N/Cl): 1 N/Kp=1 V/m, ahol V (volt) az elektrosztatikus térpotenciál mértékegysége. Ponttöltés térerőssége vákuumban (és dielektrikumban) ahol az adott térpontot q töltéssel összekötő sugárvektor. Skaláris formában: vektor irányaegybeesik a sipa irányával, pozitív töltésre hatva. Ha a mező létrejön pozitív
töltés, majd a vektor
irányította a sugárvektor mentén a töltéstől a világűrbe(teszt pozitív töltés taszítása). Ha a mező létrejön negatív töltés, majd a vektor
a töltés felé irányul(vonzerő). Grafikusan az elektrosztatikus mezőt a segítségével ábrázoljuk feszítő vonalak- olyan vonalak, amelyek érintői minden pontban egybeesnek a vektor irányával E(a) ábra). Feszültségi vonalak vannak hozzárendelve irány egybeesik a feszültségvektor irányával. Mivel a tér adott pontjában a feszültségvektornak csak egy iránya van, akkor a feszültségvonalak soha nem metszik egymást. Mert egységes mező(amikor a feszültségvektor bármely pontban állandó nagysága és iránya) a feszültségvonalak párhuzamosak a feszültségvektorral. Ha a mezőt ponttöltés hozza létre, akkor az intenzitásvonalak sugárirányú egyenesek, kimenni díjmentesen, ha pozitív, És beérkező levelek bele, ha a töltés negatív(b) ábra). 4. Áramlási vektor .
Hogy a feszítővonalak segítségével ne csak az irány, hanem az is jellemezhető legyen feszültség értéke elektrosztatikus mezővel hajtják végre egy bizonyos vastagság: a feszítővonalakra merőleges egységnyi felületen áthatoló feszítővonalak számának meg kell egyeznie a vektormodulussal .
Ekkor egy elemi területen áthatoló feszítővonalak száma dS, egyenlő hívott feszültségvektor áramlása
a platformon keresztül dS. Itt dS = dS- egy vektor, amelynek modulusa egyenlő dS, és a vektor iránya egybeesik az irányával
az oldalra. Áramlási vektor
tetszőleges zárt felületen keresztül S: Az elektrosztatikus mezők szuperpozíciójának elve. A mechanikában figyelembe véve a Coulomb-erőket alkalmazzuk az erők független fellépésének elve- eredő a mezőből a próbatöltésre ható erő egyenlő vektor összege kortyot alkalmaznak rá az egyes töltések oldaláról elektrosztatikus mezőt hozva létre. Feszültség eredő a díjrendszer által létrehozott mező is egyenlő geometriai
az egyes töltések által egy adott pontban létrehozott intenzív mezők összege. Ez a képlet kifejezi elektrosztatikus mezők szuperpozíciójának (rárakásának) elve
.
Lehetővé teszi bármely stacioner töltésrendszer elektrosztatikus mezőjének kiszámítását, ponttöltések gyűjteményeként jelenítve meg. Emlékezzünk vissza a két vektor összege vektorának nagyságának meghatározására
És
: 6. Gauss tétele.
Egy elektromos töltésrendszer térerősségének kiszámítása az elektrosztatikus mezők szuperpozíciójának elve alapján jelentősen leegyszerűsíthető a Gauss-tétel segítségével, amely meghatározza az elektromos térerősség-vektor átfolyását. bármilyen zárt felület. Tekintsük a feszültségvektor áramlását egy sugarú gömbfelületen G, pontdíj fedezése q közepén található Ez az eredmény bármely töltést körülvevő, tetszőleges alakú zárt felületre érvényes. Ha a zárt felület nem fedi a töltést, akkor az áramlás rajta nulla, mivel a felületre belépő feszítővonalak száma megegyezik az azt elhagyó feszítővonalak számával. Mérlegeljük általános eset tetszőleges n töltést körülvevő felület. A szuperpozíció elve szerint a térerő ,
Az összes töltés által létrehozott intenzitás összege egyenlő az egyes töltések által külön-külön létrehozott intenzitások összegével. Ezért Gauss tétele elektrosztatikus térre vákuumban: az elektrosztatikus térerősség vektor fluxusa vákuumban egy tetszőleges zárt felületen egyenlő a felületen belüli töltések algebrai összegével osztva. Ha a töltés térfogatsűrűséggel oszlik el a térben ,
akkor Gauss tétele: 7. A feszültségvektor cirkulációja.
Ha egy ponttöltés elektrosztatikus terében q Egy másik ponttöltés tetszőleges pályán mozog az 1. pontból a 2. pontba, ekkor a töltésre kifejtett erő működik. Erő munkája az elemi mozgásról dl egyenlő: Dolgozzon töltés mozgatásakor
az 1. ponttól a 2. pontig: Munka
nem a mozgás pályájától függ, hanem csak a kezdő- és végpontok helyzete határozza meg. Ezért a ponttöltés elektrosztatikus tere az lehetséges,
és elektrosztatikus erők - konzervatív.
Így az elektrosztatikus töltés bármely zárt áramkör mentén történő mozgatása L egyenlő nullával: Ha az átvitt díjat Mértékegység
,
majd a térerők elemi munkája az ösvényen
egyenlő
, ahol a vektor vetülete
az elemi mozgás irányába .
Integrál
hívott a feszültségvektor keringése adott L zárt körvonal mentén. Vektorcirkulációs tétel
:
Az elektrosztatikus térerősség vektor keringése bármely zárt hurok mentén nulla Erőtér, amely rendelkezik ezzel a tulajdonsággal. hívott lehetséges. Ez a képlet helyes Csak elektromos mező helyhez kötött díjak (elektrosztatikus). 8. Potenciális töltési energia.
Potenciális mezőben a testek potenciális energiával rendelkeznek, és a konzervatív erők munkája a potenciális energia elvesztése miatt történik. Ezért a munka a potenciális töltési energiák különbségeként ábrázolható q 0 a töltésmező kezdeti és végső pontjain q:
Egy töltésmezőben elhelyezkedő töltés potenciális energiája q a távolságon r egyenlő Feltételezve, hogy amikor a töltést a végtelenségig eltávolítjuk, a potenciális energia nullára megy, kapjuk: const = 0. Mert névrokon kölcsönhatásuk potenciális energiáját tölti fel (eltaszít)pozitív, Mert különböző nevek kölcsönhatásból potenciális energiát tölt fel (vonzerő)negatív. Ha a mezőt a rendszer hozza létre P ponttöltések, majd a töltés potenciális energiája d 0, amely ebben a mezőben található, egyenlő az egyes töltések által létrehozott potenciális energiák összegével: 9. Elektrosztatikus térpotenciál. Az arány nem függ a teszttöltéstől, és a mezőre jellemző energia, hívott lehetséges
:
Lehetséges
az elektrosztatikus tér bármely pontján létezik skalár az adott pontban elhelyezett egységnyi pozitív töltés potenciális energiája által meghatározott fizikai mennyiség. Például a ponttöltés által létrehozott térpotenciál q, egyenlő 10.Lehetséges különbség
Elektrosztatikus erők által végzett munka a töltés mozgatásakor
az 1. ponttól a 2. pontig úgy ábrázolható vagyis egyenlő az elmozdult töltés és a potenciálkülönbség szorzatával a kezdő és a végpontban. Lehetséges különbség Az elektrosztatikus tér két 1. és 2. pontját a térerők által végzett munka határozza meg, amikor egy egységnyi pozitív töltést 1 pontból 2. pontba mozgatnak. Az elektrosztatikus térerősség definíciójával felírhatjuk a munkát
mint ahol az integráció a kezdő- és végpontot összekötő tetszőleges vonal mentén elvégezhető, mivel az elektrosztatikus térerők munkája nem függ a mozgás pályájától. Ha mozgatja a töltést tól től tetszőleges pont a mezőn kívül
(végtelenig), ahol a potenciális energia, tehát a potenciál egyenlő nullával, akkor az elektrosztatikus tér munkája, ahonnan És így, a potenciál másik meghatározása: lehetséges
- fizikai egy olyan mennyiség, amelyet az egységnyi pozitív töltés mozgatására végzett munka határoz meg, amikor azt egy adott pontból a végtelenbe mozgatja. A potenciál mértékegysége -
volt (V): 1V a mező azon pontjának potenciálja, ahol egy 1 C töltés potenciális energiája 1 J (1 V = 1 JL C). Az elektrosztatikus mezők potenciáljainak szuperpozíciójának elve
:
Ha a mezőt több töltés hozza létre, akkor a töltésrendszer térpotenciálja egyenlő algebrai összeg mindezen töltések térpotenciálja. 11. A feszültség és a potenciál kapcsolata.
Potenciális mező esetén kapcsolat van a potenciális (konzervatív) erő és a potenciális energia között: ahol ("nabla") - Hamilton operátor
: Azóta és azóta A mínusz jel azt jelzi, hogy a vektor
oldalra irányítva ereszkedő lehetséges. 12. Potenciális felületek.
A potenciáleloszlás grafikus megjelenítéséhez ekvipotenciális felületeket használnak - olyan felületeket, amelyek minden pontján a potenciál azonos értékű. Az ekvipotenciálfelületeket általában úgy rajzolják meg, hogy két szomszédos ekvipotenciálfelület közötti potenciálkülönbség azonos legyen. Ekkor az ekvipotenciális felületek sűrűsége egyértelműen jellemzi a térerősséget a különböző pontokon. Ahol ezek a felületek sűrűbbek, ott nagyobb a térerősség. Az ábrán a szaggatott vonal az erővonalakat, a folytonos vonalak az ekvipotenciális felületek metszeteit mutatja: pozitív ponttöltés (A), dipólus (b), két hasonló töltés (V),összetett konfigurációjú töltött fémvezető (G). Ponttöltés esetén a potenciál , tehát az ekvipotenciális felületek koncentrikus gömbök. Másrészt a feszítővonalak radiális egyenesek. Következésképpen a feszültségvonalak merőlegesek az ekvipotenciális felületekre. Meg lehet mutatni, hogy minden esetben 1) vektor merőleges ekvipotenciális felületek és 2) mindig a potenciál csökkentésére irányul. 13.Példák a legfontosabb szimmetrikus elektrosztatikus mezők számításaira vákuumban.
1. Elektromos dipólus elektrosztatikus tere vákuumban.
Elektromos dipólus(vagy kettős villanypólus) két egyenlő nagyságú ellentétes ponttöltésből álló rendszer (+q,-q), távolság l amelyek között lényegesen kisebb a távolság a mező figyelembe vett pontjaitól ( l< Dipólus kar
- a dipólus tengelye mentén negatív töltésről pozitívra irányított vektor, amely egyenlő a köztük lévő távolsággal. Elektromos dipólusmomentum p e- egy vektor, amely egybeesik a dipólus karjával, és egyenlő a töltési modulus és a kar szorzatával: Hadd r- távolság az A ponttól a dipólus tengelyének közepétől. Akkor, tekintettel arra r>>l. 2) Térerő a merőleges B pontjában, középpontjából visszaállítva a dipólustengelyre r'>>l. Ezért Szuperpozíció elve Tegyük fel, hogy hárompontos töltésünk van. Ezek a díjak kölcsönhatásba lépnek. Kísérletet végezhet, és megmérheti az egyes töltésekre ható erőket. Ahhoz, hogy megtaláljuk a teljes erőt, amellyel a második és a harmadik egy töltésre hat, össze kell adni azokat az erőket, amelyekkel mindegyik a paralelogramma szabálya szerint hat. Felmerül a kérdés, hogy az egyes töltésekre ható mért erő egyenlő-e a másik kettő által kifejtett erők összegével, ha az erőket a Coulomb-törvény szerint számítjuk. Kutatások kimutatták, hogy a mért erő egyenlő a Coulomb-törvény szerint számított erők összegével két töltésre vonatkoztatva. Ezt az empirikus eredményt állítások formájában fejezzük ki: Ezt az állítást szuperpozíció elvének nevezzük. Ez az elv az elektromosság tanának egyik alapja. Ez ugyanolyan fontos, mint a Coulomb-törvény. Nyilvánvaló az általánosítás sok vád esetére. Ha több térforrás van (a töltések száma N), akkor a q teszttöltésre ható erő a következőképpen határozható meg: \[\overrightarrow(F)=\sum\limits^N_(i=1)(\overrightarrow(F_(ia)))\left(1\right),\] ahol $\overrightarrow(F_(ia))$ az az erő, amellyel a $q_i$ töltés hat a q töltésre, ha nincs más N-1 töltés. A szuperpozíció elve (1) lehetővé teszi a ponttöltések közötti kölcsönhatás törvényének felhasználásával, hogy kiszámítsuk a véges méretű testen elhelyezkedő töltések közötti kölcsönhatás erejét. Ehhez minden töltést fel kell osztani kis dq töltésekre, amelyek ponttöltésnek tekinthetők, párosítva kell őket felvenni, kiszámítani a kölcsönhatási erőt és a keletkező erők vektoros összeadását végezni. A szuperpozíció elvének van térértelmezése: két ponttöltés térereje egyenlő azoknak az intenzitásoknak az összegével, amelyeket az egyes töltések hoznak létre, a másik hiányában. Általában a feszültségekre vonatkozó szuperpozíció elve a következőképpen írható le: \[\overrightarrow(E)=\sum(\overrightarrow(E_i))\left(2\right).\] ahol $(\overrightarrow(E))_i=\frac(1)(4\pi (\varepsilon )_0)\frac(q_i)(\varepsilon r^3_i)\overrightarrow(r_i)\ $ a i-edik töltés, a $\overrightarrow(r_i)\ $ az i-edik töltésből a tér egy pontjába húzott sugárvektor. Az (1) kifejezés azt jelenti, hogy tetszőleges számú ponttöltés térerőssége megegyezik az egyes ponttöltések térerősségének összegével, ha nincs más. A mérnöki gyakorlat megerősítette, hogy a szuperpozíció elvét nagyon nagy térerősségig betartják. Az atomokban és az atommagokban lévő mezők erőssége igen jelentős ($(10)^(11)-(10)^(17)\frac(B)(m)$, de még ezeknél is érvényesül a szuperpozíció elve. Az atomok energiaszintjének kiszámításához használtuk, és a számítási adatok nagy pontossággal egybeestek a kísérleti adatokkal. Meg kell azonban jegyezni, hogy nagyon kis távolságok ($\sim (10)^(-15)m$ nagyságrendű) és rendkívül erős mezők esetén előfordulhat, hogy a szuperpozíció elve nem érvényesül. Így például nehéz atommagok felületén az erősségek elérik a $\sim (10)^(22)\frac(V)(m)$ nagyságrendet, a szuperpozíciós elv teljesül, de $(10) erősségnél )^(20)\frac(V )(m)$ kvantum - kölcsönhatás mechanikai nemlinearitásai keletkeznek. Ha a töltés folyamatosan eloszlik (nem kell figyelembe venni a diszkrétséget), akkor a teljes térerősséget a következőképpen kapjuk meg: \[\overrightarrow(E)=\int(d\overrightarrow(E))\ \left(3\right).\] A (3) egyenletben az integrációt a töltéseloszlási tartományon keresztül hajtjuk végre. Ha a töltések a vonal mentén oszlanak el ($\tau =\frac(dq\ )(dl)-linear\ density\ eloszlás\töltés$), akkor a (3)-ba való integráció a vonal mentén történik. Ha a töltések eloszlanak a felületen, és a felületi eloszlás sűrűsége $\sigma =\frac(dq\ )(dS)$, akkor integrálja a felületet. Térfogat feletti integrációt hajtunk végre, ha térfogati töltéseloszlással foglalkozunk: $\rho =\frac(dq\ )(dV)$, ahol $\rho$ a térfogati töltéseloszlás sűrűsége. A szuperpozíció elve elvileg lehetővé teszi a $\overrightarrow(E)$ meghatározását a tér bármely pontjára egy ismert térbeli töltéseloszlásból. 1. példa Feladat: Az a oldalú négyzet csúcsaiban azonos q ponttöltések találhatók. Határozza meg az egyes töltésekre a másik három töltés által kifejtett erőt! Ábrázoljuk az egyik töltésre ható erőket a négyzet csúcsában (a választás nem fontos, mivel a töltések azonosak) (1. ábra). A $q_1$ töltésre ható erőt a következőképpen írjuk fel: \[\overrightarrow(F)=(\overrightarrow(F))_(12)+(\overrightarrow(F))_(14)+(\overrightarrow(F))_(13)\ \left(1.1\right ).\] A $(\overrightarrow(F))_(12)$ és $(\overrightarrow(F))_(14)$ erők egyenlő nagyságúak, és a következőképpen találhatók meg: \[\left|(\overrightarrow(F))_(12)\right|=\left|(\overright arrow(F))_(14)\right|=k\frac(q^2)(a^2) )\ \left(1,2\right),\] ahol $k=9 (10)^9\frac(Nm^2)((C)^2).$ Meg fogjuk találni a $(\overrightarrow(F))_(13)$ erőmodulust, szintén Coulomb törvénye szerint, tudva, hogy a négyzet átlója egyenlő: ezért nekünk van: \[\left|(\overrightarrow(F))_(13)\right|=k\frac(q^2)(2a^2)\ \left(1,4\right)\] Irányítsuk az OX tengelyt az ábra szerint. 1, vetítjük az (1.1) egyenletet, behelyettesítjük a kapott erőmodulokat, így kapjuk: Válasz: A négyzet csúcsaiban lévő töltésekre ható erő egyenlő: $F=\frac(kq^2)(a^2)\left(\frac(2\sqrt(2)+1) (2)\jobbra) .$ 2. példa Feladat: Az elektromos töltés egyenletesen oszlik el egy vékony menet mentén, amelynek lineáris sűrűsége $\tau$. Keressen kifejezést a térerősségre a szál végétől $a$ távolságban annak folytatása mentén. A szál hossza $l$. Válasszunk ki egy $dq$ ponttöltést a meneten, és írjuk rá a Coulomb-törvényből az elektrosztatikus térerősség kifejezését: Egy adott pontban minden feszültségvektor egyformán, az X tengely mentén irányul, ezért van: Mivel a töltés a probléma körülményei szerint egyenletesen oszlik el a meneten $\tau $ lineáris sűrűséggel, a következőket írhatjuk: Helyettesítsük be (2.4)-et a (2.1) egyenletbe, és integráljuk: Válasz: A menet térerősségét a jelzett pontban a következő képlettel számítjuk ki: $E=\frac(k\tau l)(a(l+a)).$ A mezők szuperpozíciójának (átfedésének) elve a következőképpen van megfogalmazva: Ha a tér egy adott pontjában különböző töltött részecskék elektromos mezőket hoznak létre, amelyek erősségei stb., akkor a kapott térerősség ebben a pontban egyenlő: . A mezőszuperpozíció elve arra az esetre érvényes, amikor a több különböző töltés által létrehozott mezők semmilyen hatást nem gyakorolnak egymásra, vagyis úgy viselkednek, mintha nem lennének más mezők. A tapasztalatok azt mutatják, hogy a természetben előforduló közönséges intenzitású mezők esetében ez valóban előfordul. A szuperpozíció elvének köszönhetően egy töltött részecskék rendszerének térerősségének bármely pontban történő meghatározásához elegendő a ponttöltés térerősségének kifejezést használni. Az alábbi ábra azt mutatja, hogyan az adott ponton A két ponttöltés által létrehozott térerősséget határozzuk meg q 1
És q 2. Az elektromos teret a térben általában erővonalak ábrázolják. Az erővonalak fogalmát M. Faraday vezette be a mágnesesség tanulmányozása során. Ezt a koncepciót azután J. Maxwell dolgozta ki az elektromágnesességgel kapcsolatos kutatásai során. Az erővonal vagy az elektromos térerősség vonala olyan egyenes, amelynek minden pontjának érintője egybeesik a mező ezen pontjában található pozitív ponttöltésre ható erő irányával. Az alábbi ábrák egy pozitív töltésű golyó feszültségvonalait mutatják (1. ábra); két különböző töltésű golyó (2. ábra); két hasonló töltésű golyó (3. ábra) és két különböző előjelű, de abszolút értékben azonos töltéssel töltött lemez (4. ábra). Az utolsó ábrán látható feszültségvonalak a lemezek közötti térben szinte párhuzamosak, sűrűségük azonos. Ez arra utal, hogy a tér ebben a régiójában egységes a mező. Az elektromos teret homogénnek nevezzük, ha ereje a tér minden pontjában azonos. Az elektrosztatikus térben az erővonalak nem zártak, mindig pozitív töltésekkel kezdődnek és negatív töltésekkel végződnek. Nem metszik egymást sehol, a térvonalak metszéspontja a térerő irányának bizonytalanságát jelezné a metszéspontban. A térvonalak sűrűsége nagyobb töltött testek közelében, ahol nagyobb a térerősség. Egy töltött vezető golyó térerőssége a golyó középpontjától a sugarát meghaladó távolságban r ≥
R. ugyanaz a képlet határozza meg, mint a ponttöltés mezőit A labda töltete egyenletesen oszlik el a felületén. A vezető labdán belül a térerősség nulla.




Szuperpozíció elve
A szuperpozíció elvének terepi értelmezése
2. definíció 
![]() kg. Az elemi pozitív töltés hordozója az proton. A tömege
kg. Az elemi pozitív töltés hordozója az proton. A tömege ![]() kg.
kg.
Bármely zárt elektromos töltés algebrai összege
a rendszer változatlan marad, függetlenül attól, hogy milyen folyamatok fordulnak elő
ezen a rendszeren belül.![]()
![]()
![]() vagy
vagy ![]() . Akkor
. Akkor ![]()
![]()
![]()




![]() Ahol
- vektoros vetítés tovább Normál
az oldalra dS. (Vektor
- a helyszínre merőleges egységvektor dS). Nagyságrend
Ahol
- vektoros vetítés tovább Normál
az oldalra dS. (Vektor
- a helyszínre merőleges egységvektor dS). Nagyságrend![]()

![]()
![]()



![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()



![]()

A szuperpozíció elvének terepi értelmezése



Elektromos erővonalak.
Egy feltöltött labda mezője.
 . Ezt bizonyítja a mezővonalak eloszlása (ábra). A), hasonlóan egy ponttöltés intenzitásvonalainak eloszlásához (ábra. b).
. Ezt bizonyítja a mezővonalak eloszlása (ábra). A), hasonlóan egy ponttöltés intenzitásvonalainak eloszlásához (ábra. b).