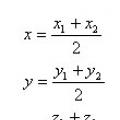- Coordinates of the midpoint of the segment.
Lesson Objectives
- Expand your horizons of concepts.
- Get acquainted with new definitions and remember some already studied.
- Learn to apply the properties of shapes when solving problems.
- Developmental – to develop students’ attention, perseverance, perseverance, logical thinking, mathematical speech.
- Educational - through the lesson, cultivate an attentive attitude towards each other, instill the ability to listen to comrades, mutual assistance, and independence.
Lesson Objectives
- Test students' problem-solving skills.
Lesson Plan
- Introduction.
- Repetition of previously studied material.
- Coordinates of the midpoint of the segment.
- Logic problems.
introduction
Before moving on to the material on the topic itself, I would like to talk a little about a segment not only as a mathematical definition. Many scientists have tried look at the segment differently, saw something unusual in him. Some talented artists made geometric shapes convey mood and emotions.
There are many theories about how color affects our mood and why.
Color can be felt and is closely related to our emotions. The color of nature, architecture, plants, clothing that surrounds us gradually affects our mood.
According to experts, colors can affect a person.
- Red color can lift your spirits and give you strength.
- Pink the color symbolizes peace and tranquility.
- Orange is a warm, restless color that gives energy and lifts the mood.
- In Imperial China yellow was considered such a sacred color that only the emperor could wear yellow clothes. The Egyptians and Mayans considered yellow to be the color of the Sun and revered its life-sustaining power. Yellow flowers can invigorate and bring joy when you are not feeling well.
- Green- healing color. Causes a feeling of balance and harmony.
- Blue enhances creativity.
- Violet- the color of thoughtfulness, spirituality and peace. It is associated with intuition and caring for others.
- White usually considered the color of purity and innocence. It is also associated with inspiration, insight, spirituality and love.
But there are so many people and so many opinions. Everyone has their own truth.
There is also an interesting theory about how it is connected the shape of a line or segment with its character.
Shape, like color, is a property of an object. Form- these are the external outlines of a visible object, reflecting its spatial aspects (forma, translated from Latin - external appearance). Everything that surrounds us has a certain shape. Understanding and depicting its structural structure and semantic content is the artist’s task. And we, as viewers, need to be able to read the image, decipher the nature and meaning of various forms. On a sheet of paper and a computer screen, a shape is formed when a line is closed. Therefore, the nature of the form depends on the nature of the line by which it is formed.
Which of these lines can express calm, anger, indifference, excitement, joy?
There can be no clear answer in this case. For example, a prickly line can express anger, gloating or wild joy bordering on recklessness.
What mood or emotion corresponds to each of these lines?
How does a form depend on the nature of the line by which it is formed?
Repetition of previously studied material
In space
There are two arbitrary points A1(x 1 ;y 1 ;z 1) and A2(x 2 ;y 2 ;z 2). Then the midpoint of segment A1A2 will be the point WITH with coordinates x, y, z, where

Dividing a segment in a given ratio
If x 1 and y 1 are the coordinates of point A, and x 2 and y 2 are the coordinates of point B, then the x and y coordinates of point C, dividing the segment AB in relation to , are determined by the formulas
The area of a triangle based on the known coordinates of its vertices A(x 1, y 1), B(x 2, y 2), C(x 3, y 3) is calculated by the formula.
The number obtained using this formula should be taken in absolute value.
Example No. 1
Find the midpoint of segment AB.

Answer: The coordinates of the middle of the segment are (1.5;2)
Example No. 2.
Find the midpoint of segment AB.
Answer: The coordinates of the middle of the segment are equal to (21;0)
Example No. 3.
Find the coordinates of point C if AC=5.5 and CB=19.5.
A(1;7), B(43;-4)

Answer: Coordinates of point C(10.24;4.58)
Tasks
Task No. 1
Find the midpoint of segment DB.

Task No. 2.
Find the middle of the segment CD.

How statues are made.
It is said about many famous sculptors that when asked how they manage to make such wonderful statues, the answer was: “I take a block of marble and cut off everything unnecessary from it.” You can read this in different books about Michelangelo, about Thorvaldsen, about Rodin.


In the same way, you can get any limited flat geometric figure: you need to take some square in which it lies, and then cut off all that is unnecessary. However, it is necessary to cut off not immediately, but gradually, at each step discarding a piece shaped like a circle. In this case, the circle itself is thrown away, and its border - the circle - remains in the figure.
At first glance, it seems that only figures of a certain type can be obtained this way. But the whole point is that they discard not one or two circles, but an infinite, or more precisely, a countable set of circles. In this way you can get any figure. To be convinced of this, it is enough to take into account that the set of circles for which both the radius and both coordinates of the center are rational is countable.
And now, to get any figure, it is enough to take the square containing it (a block of marble) and draw all the circles of the above type that do not contain a single point of the figure we need. If you throw circles not from a square, but from the entire plane, then using the described technique you can obtain unlimited figures.
Questions
- What is a segment?
- What does the segment consist of?
- How can you find the midpoint of a segment?
List of sources used
- Kuznetsov A.V., mathematics teacher (grades 5-9), Kiev
- “Unified State Exam 2006. Mathematics. Educational and training materials for preparing students / Rosobrnadzor, ISOP - M.: Intellect-Center, 2006"
- Mazur K. I. “Solving the main competition problems in mathematics of the collection edited by M. I. Skanavi”
- L. S. Atanasyan, V. F. Butuzov, S. B. Kadomtsev, E. G. Poznyak, I. I. Yudina “Geometry, 7 – 9: textbook for educational institutions”
We worked on the lesson
Kuznetsov A.V.
Poturnak S.A.
Tatyana Prosnyakova
Introduction of Cartesian coordinates in space. Distance between points. Coordinates of the midpoint of the segment.
Lesson objectives:
Educational: Consider the concept of a coordinate system and the coordinates of a point in space; derive the distance formula in coordinates; derive the formula for the coordinates of the midpoint of the segment.
Educational: To promote the development of students' spatial imagination; contribute to the development of problem solving and the development of logical thinking of students.
Educational: Fostering cognitive activity, a sense of responsibility, a culture of communication, a culture of dialogue.
Equipment: Drawing supplies, presentation, digital design center
Lesson type: Lesson on learning new material
Lesson structure:
Organizing time.
Updating basic knowledge.
Learning new material.
Updating new knowledge
Lesson summary.
During the classes
Message from history " Cartesian coordinate system"(Learner)
When solving a geometric, physical, chemical problem, you can use various coordinate systems: rectangular, polar, cylindrical, spherical.
In the general education course, the rectangular coordinate system on the plane and in space is studied. Otherwise, it is called the Cartesian coordinate system after the French scientist philosopher Rene Descartes (1596 - 1650), who first introduced coordinates into geometry.
(Student's story about Rene Descartes.)
Rene Descartes was born in 1596 in the city of Lae in the south of France, into a noble family. My father wanted to make Rene an officer. To do this, in 1613 he sent Rene to Paris. Descartes had to spend many years in the army, participating in military campaigns in Holland, Germany, Hungary, the Czech Republic, Italy, and in the siege of the Huguenot fortress of La Rochalie. But Rene was interested in philosophy, physics and mathematics. Soon after his arrival in Paris, he met Vieta's student, a prominent mathematician of that time - Mersen, and then other mathematicians in France. While in the army, Descartes devoted all his free time to mathematics. He studied German algebra and French and Greek mathematics.
After the capture of La Rochalie in 1628, Descartes left the army. He leads a solitary life in order to implement his extensive plans for scientific work.
Descartes was the greatest philosopher and mathematician of his time. Descartes' most famous work is his Geometry. Descartes introduced a coordinate system that everyone uses today. He established a correspondence between numbers and line segments and thus introduced the algebraic method into geometry. These discoveries of Descartes gave a huge impetus to the development of both geometry and other branches of mathematics and optics. It became possible to depict the dependence of quantities graphically on the coordinate plane, numbers - as segments, and to perform arithmetic operations on segments and other geometric quantities, as well as various functions. It was a completely new method, distinguished by beauty, grace and simplicity.
Repetition. Rectangular coordinate system on a plane.
Questions:
What is called a coordinate system on a plane?
How are the coordinates of a point on a plane determined?
What are the coordinates of the origin?
What is the formula for the coordinates of the midpoint of a segment and the distance between points on a plane?
Learning new material:
A rectangular coordinate system in space is a trio of mutually perpendicular coordinate lines with a common origin. The common origin is denoted by the letterO.
Oh - abscissa axis,
Oy – ordinate axis,
ABOUTz– applicate axis

Three planes passing through the coordinate axes Ox and Oy, Oy and Oz, ABOUTzand Ox are called coordinate planes: Oxy, Oyz, ABOUTzX.
In a rectangular coordinate system, each point M in space is associated with a triple of numbers - its coordinates.
M(x,y,z), where x is the abscissa, y is the ordinate,z- applicate.
Coordinate system in space


Point coordinates

Distance between points

1 (x 1 ;y 1 ;z 1 ) and A 2 (x 2 ;y 2 ;z 2 )
Then the distance between points A 1 and A 2 is calculated like this:
Coordinates of the midpoint of the segment in space
There are two arbitrary points A 1 (x 1 ;y 1 ;z 1 ) and A 2 (x 2 ;y 2 ;z 2 ). Then the midpoint of the segment A 1 A 2 there will be a point C with coordinates x, y, z, where

Gaining solution skills:
1) Find the coordinates of the orthogonal projections of the pointsA (1, 3, 4) and
B (5, -6, 2) to:
a) planeOxy ; b) planeOyz ; c) axisOx ; d) axisOz .
Answer: a) (1, 3, 0), (5, -6, 0); b) (0, 3, 4), (0, -6, 2); c) (1, 0, 0), (5, 0, 0);
d) (0, 0, 4), (0, 0, 2).
2) At what distance is the pointA (1, -2, 3) from the coordinate plane:
A)Oxy ; b)Oxz ; V)Oyz ?
Answer: a) 3; b) 2; in 1
3) Find the coordinates of the middle of the segment:
A)AB , IfA (1, 2, 3) andB (-1, 0, 1); b)CD , IfC (3, 3, 0) andD (3, -1, 2).
Answer: a) (1, 1, 2); b) (3, 1, 1).
5. Homework: textbook by A.V. Pogorelov “Geometry 10-11” pp. 23 – 25, p. 53 answer questions No. 1 – 3; №7, №10(1)
6. Lesson summary.
Table
On surfaceIn space
Definition. A coordinate system is a set of two intersecting coordinate axes, the point at which these axes intersect - the origin - and unit segments on each of the axes
Definition. A coordinate system is a set of three coordinate axes, the point at which these axes intersect - the origin of coordinates - and unit segments on each of the axes
2 axles,
OU - ordinate axis,
OX - abscissa axis
3 axles,
OX - abscissa axis,
OU – ordinate axis,
OZ - applicator axis.
OX is perpendicular to OA
OX is perpendicular to OU,
OX is perpendicular to OZ,
Op-amp is perpendicular to OZ
(O;O)
(OOO)
Direction, single segment
Distance between points.
Distance between points
Coordinates of the midpoint of the segment.
Coordinates of the midpoint of the segment
Questions:
How is the Cartesian coordinate system introduced? What does it consist of?
How are the coordinates of a point in space determined?
What is the coordinate of the point of intersection of the coordinate axes?
What is the distance from the origin to a given point?
What is the formula for the coordinates of the middle of a segment and the distance between points in space?
Student assessment
7.Reflection
At the lesson
I found out …
I learned…
I like it…
I found it difficult...
My mood…
Literature.
A.V. Pogorelov. Textbook 10-11. M. “Enlightenment”, 2010.
I.S. Petrakov. Math clubs in grades 8-10. M, “Enlightenment”, 1987
There is a whole group of tasks (included in exam types of problems) associated with the coordinate plane. These are problems ranging from the most basic ones, which are solved orally (determining the ordinate or abscissa of a given point, or a symmetrical point to a given point, and others), ending with tasks that require high-quality knowledge, understanding and good skills (problems related to the angular coefficient of a straight line).
Gradually we will consider all of them. In this article, we'll start with the basics. These are simple tasks to determine: the abscissa and ordinate of a point, the length of a segment, the midpoint of a segment, the sine or cosine of the slope of a straight line.Most people will not be interested in these tasks. But I consider it necessary to present them.
The fact is that not everyone goes to school. Many people take the Unified State Exam 3-4 or more years after graduation, and they vaguely remember what the abscissa and ordinate are. We will also analyze other tasks related to the coordinate plane, don’t miss it, subscribe to blog updates. Now n a little theory.
Let's construct point A on the coordinate plane with coordinates x=6, y=3.

They say that the abscissa of point A is equal to six, the ordinate of point A is equal to three.
To put it simply, the ox axis is the abscissa axis, the y axis is the ordinate axis.
That is, the abscissa is a point on the x axis into which a point given on the coordinate plane is projected; The ordinate is the point on the y axis to which the specified point is projected.
Length of a segment on the coordinate plane
Formula for determining the length of a segment if the coordinates of its ends are known:

As you can see, the length of a segment is the length of the hypotenuse in a right triangle with equal legs
X B - X A and U B - U A
* * *
The middle of the segment. Her coordinates.

Formula for finding the coordinates of the midpoint of a segment:

Equation of a line passing through two given points

The formula for the equation of a straight line passing through two given points has the form:

where (x 1;y 1) and (x 2;y 2 ) coordinates of given points.
Substituting the coordinate values into the formula, it is reduced to the form:
y = kx + b, where k is the slope of the line
We will need this information when solving another group of problems related to the coordinate plane. There will be an article about this, don’t miss it!
What else can you add?
The angle of inclination of a straight line (or segment) is the angle between the oX axis and this straight line, ranging from 0 to 180 degrees.

Let's consider the tasks.
From the point (6;8) a perpendicular is dropped onto the ordinate axis. Find the ordinate of the base of the perpendicular.

The base of the perpendicular lowered onto the ordinate axis will have coordinates (0;8). The ordinate is equal to eight.
Answer: 8
Find the distance from the point A with coordinates (6;8) to the ordinate.

The distance from point A to the ordinate axis is equal to the abscissa of point A.
Answer: 6.
A(6;8) relative to the axis Ox.

A point symmetrical to point A relative to the oX axis has coordinates (6;– 8).

The ordinate is equal to minus eight.
Answer: – 8
Find the ordinate of a point symmetrical to the point A(6;8) relative to the origin.

A point symmetrical to point A relative to the origin has coordinates (– 6;– 8).
Its ordinate is – 8.

Answer: –8
Find the abscissa of the midpoint of the segment connecting the pointsO(0;0) and A(6;8).

In order to solve the problem, it is necessary to find the coordinates of the middle of the segment. The coordinates of the ends of our segment are (0;0) and (6;8).
We calculate using the formula:

We got (3;4). The abscissa is equal to three.
Answer: 3
*The abscissa of the middle of a segment can be determined without calculation using a formula by constructing this segment on a coordinate plane on a sheet of paper in a square. The middle of the segment will be easy to determine by the cells.
Find the abscissa of the midpoint of the segment connecting the points A(6;8) and B(–2;2).

In order to solve the problem, it is necessary to find the coordinates of the middle of the segment. The coordinates of the ends of our segment are (–2;2) and (6;8).
We calculate using the formula:

We got (2;5). The abscissa is equal to two.
Answer: 2
*The abscissa of the middle of a segment can be determined without calculation using a formula by constructing this segment on a coordinate plane on a sheet of paper in a square.
Find the length of the segment connecting the points (0;0) and (6;8).

The length of the segment at the given coordinates of its ends is calculated by the formula:

in our case we have O(0;0) and A(6;8). Means,
*The order of coordinates when subtracting does not matter. You can subtract the abscissa and ordinate of point A from the abscissa and ordinate of point O:
Answer:10
Find the cosine of the slope of the segment connecting the points O(0;0) and A(6;8), with x-axis.

The angle of inclination of a segment is the angle between this segment and the oX axis.
From point A we lower a perpendicular to the oX axis:

That is, the angle of inclination of a segment is the angleSAIin right triangle ABO.
The cosine of an acute angle in a right triangle is
ratio of adjacent leg to hypotenuse

We need to find the hypotenuseOA.
According to the Pythagorean theorem:In a right triangle, the square of the hypotenuse is equal to the sum of the squares of the legs.

Thus, the cosine of the slope angle is 0.6
Answer: 0.6
From point (6;8) a perpendicular is dropped onto the abscissa axis. Find the abscissa of the base of the perpendicular.

A straight line parallel to the abscissa axis is drawn through the point (6;8). Find the ordinate of its intersection point with the axis OU.

Find the distance from the point A with coordinates (6;8) to the abscissa axis.

Find the distance from the point A with coordinates (6;8) to the origin.

Let A(X 1; y 1) and B(x 2; y 2) be two arbitrary points and C (x; y) be the midpoint of the segment AB. Let's find the x, y coordinates of point C.
Let us first consider the case when the segment AB is not parallel to the y-axis, i.e. X 1 X 2. Let us draw straight lines through points A, B, C, parallel to the y-axis (Fig. 173). They will intersect the x axis at points A 1 (X 1; 0), B 1 (X 2; 0), C 1 (x; 0). According to Thales' theorem, point C 1 will be the midpoint of the segment A 1 B 1.

Since point C 1 is the middle of the segment AiBi, then A 1 C 1 = B 1 C 1, which means Ix - X 1 I = Ix - X 2 I. It follows that either x - x 1 = x - x 2 , or (x - x 1) = -(x-x 2).
The first equality is impossible, since x 1 x 2. Therefore the second is true. And from this we get the formula
If x 1 = x 2, that is, the segment AB is parallel to the y-axis, then all three points A 1, B 1, C 1 have the same abscissa. This means that the formula remains true in this case.
The ordinate of point C is found similarly. Through points A, B, C, straight lines are drawn parallel to the x axis. The formula turns out to be
Problem (15). Given three vertices of parallelogram ABCD: A (1; 0), B (2; 3), C (3; 2). Find the coordinates of the fourth vertex D and the intersection points of the diagonals.
Solution. The point of intersection of the diagonals is the midpoint of each of them. Therefore, it is the midpoint of the segment AC, which means it has coordinates
![]()
Now, knowing the coordinates of the point of intersection of the diagonals, we find the coordinates x, y of the fourth vertex D. Using the fact that the point of intersection of the diagonals is the midpoint of the segment BD, we have:

A. V. Pogorelov, Geometry for grades 7-11, Textbook for educational institutions
After painstaking work, I suddenly noticed that the size of web pages is quite large, and if things continue like this, then I can quietly go wild =) Therefore, I bring to your attention a short essay dedicated to a very common geometric problem - about dividing a segment in this respect, and, as a special case, about dividing a segment in half.
For one reason or another, this task did not fit into other lessons, but now there is a great opportunity to consider it in detail and leisurely. The good news is that we'll take a break from vectors and focus on points and segments.
Formulas for dividing a segment in this regardThe concept of dividing a segment in this regard
The concept of dividing a segment in this regard
Often you don’t have to wait for what’s promised at all; let’s immediately look at a couple of points and, obviously, the incredible – the segment:
The problem under consideration is valid both for segments of the plane and for segments of space. That is, the demonstration segment can be placed as desired on a plane or in space. For ease of explanation, I drew it horizontally.
What are we going to do with this segment? This time to cut. Someone is cutting a budget, someone is cutting a spouse, someone is cutting firewood, and we will start cutting the segment into two parts. The segment is divided into two parts using a certain point, which, of course, is located directly on it:
In this example, the point divides the segment in such a way that the segment is half as long as the segment. You can ALSO say that a point divides a segment in a ratio (“one to two”), counting from the vertex.
In dry mathematical language, this fact is written as follows: , or more often in the form of the usual proportion: . The ratio of segments is usually denoted by the Greek letter “lambda”, in this case: .
It is easy to compose the proportion in a different order: - this notation means that the segment is twice as long as the segment, but this does not have any fundamental significance for solving problems. It can be like this, or it can be like that.
Of course, the segment can easily be divided in some other respect, and to reinforce the concept, the second example:
Here the following ratio is valid: . If we make the proportion the other way around, then we get: .
After we have figured out what it means to divide a segment in this respect, we move on to considering practical problems.
If two points of the plane are known, then the coordinates of the point that divides the segment in relation to are expressed by the formulas: ![]()
Where did these formulas come from? In the course of analytical geometry, these formulas are strictly derived using vectors (where would we be without them? =)). In addition, they are valid not only for the Cartesian coordinate system, but also for an arbitrary affine coordinate system (see lesson Linear (non) dependence of vectors. Basis of vectors). This is such a universal task.
Example 1
Find the coordinates of the point dividing the segment in the relation if the points are known ![]()
Solution: In this problem. Using the formulas for dividing a segment in this relation, we find the point: 
Answer:
Pay attention to the calculation technique: first you need to separately calculate the numerator and the denominator separately. The result is often (but not always) a three- or four-story fraction. After this, we get rid of the multi-story structure of the fraction and carry out the final simplifications.
The task does not require drawing, but it is always useful to do it in draft form:

Indeed, the relation is satisfied, that is, the segment is three times shorter than the segment . If the proportion is not obvious, then the segments can always be stupidly measured with an ordinary ruler.
Equally valuable second solution: in it the countdown starts from a point and the following relation is fair: ![]() (in human words, a segment is three times longer than a segment ). According to the formulas for dividing a segment in this respect:
(in human words, a segment is three times longer than a segment ). According to the formulas for dividing a segment in this respect: 
Answer:
Please note that in the formulas it is necessary to move the coordinates of the point to the first place, since the little thriller began with it.
It is also clear that the second method is more rational due to simpler calculations. But still, this problem is often solved in the “traditional” manner. For example, if according to the condition a segment is given, then it is assumed that you will make up a proportion; if a segment is given, then the proportion is “tacitly” implied.
And I gave the second method for the reason that often they try to deliberately confuse the conditions of the problem. That is why it is very important to carry out a rough drawing in order, firstly, to correctly analyze the condition, and, secondly, for verification purposes. It's a shame to make mistakes in such a simple task.
Example 2
Points given ![]() . Find:
. Find:
a) a point dividing the segment in relation to ;
b) a point dividing the segment in relation to .
This is an example for you to solve on your own. Full solution and answer at the end of the lesson.
Sometimes there are problems where one of the ends of the segment is unknown:
Example 3
The point belongs to the segment. It is known that a segment is twice as long as a segment. Find the point if ![]() .
.
Solution: From the condition it follows that the point divides the segment in the ratio , counting from the vertex, that is, the proportion is valid: . According to the formulas for dividing a segment in this respect: ![]()
Now we do not know the coordinates of the point :, but this is not a particular problem, since they can be easily expressed from the above formulas. It doesn’t cost anything to express in general terms; it’s much easier to substitute specific numbers and carefully figure out the calculations: 
Answer:
To check, you can take the ends of the segment and, using formulas in direct order, make sure that the relationship actually results in a point. And, of course, of course, a drawing will not be superfluous. And in order to finally convince you of the benefits of a checkered notebook, a simple pencil and a ruler, I propose a tricky problem for you to solve on your own:
Example 4
Dot . The segment is one and a half times shorter than the segment. Find a point if the coordinates of the points are known ![]() .
.
The solution is at the end of the lesson. By the way, it is not the only one; if you follow a different path from the sample, it will not be a mistake, the main thing is that the answers match.
For spatial segments everything will be exactly the same, only one more coordinate will be added.
If two points in space are known, then the coordinates of the point that divides the segment in relation to are expressed by the formulas:
.
Example 5
Points are given. Find the coordinates of a point belonging to the segment if it is known that ![]() .
.
Solution: The condition implies the relation: ![]() . This example was taken from a real test, and its author allowed himself a little prank (in case someone stumbles) - it would have been more rational to write the proportion in the condition like this:
. This example was taken from a real test, and its author allowed himself a little prank (in case someone stumbles) - it would have been more rational to write the proportion in the condition like this: ![]() .
.
According to the formulas for the coordinates of the midpoint of the segment:
Answer: ![]()
3D drawings for inspection purposes are much more difficult to produce. However, you can always make a schematic drawing to understand at least the condition - which segments need to be correlated.
As for fractions in the answer, don’t be surprised, it’s a common thing. I’ve said it many times, but I’ll repeat it: in higher mathematics it is customary to use ordinary regular and improper fractions. The answer is in the form ![]() will do, but the option with improper fractions is more standard.
will do, but the option with improper fractions is more standard.
Warm-up task for independent solution:
Example 6
Points are given. Find the coordinates of the point if it is known that it divides the segment in the ratio.
The solution and answer are at the end of the lesson. If it is difficult to navigate the proportions, make a schematic drawing.
In independent and test work, the examples considered are found both on their own and as an integral part of larger tasks. In this sense, the problem of finding the center of gravity of a triangle is typical.
I don’t see much point in analyzing the type of task where one of the ends of the segment is unknown, since everything will be similar to the flat case, except that there are a little more calculations. Let’s remember our school years better:
Formulas for the coordinates of the midpoint of a segment
Even untrained readers can remember how to divide a segment in half. The problem of dividing a segment into two equal parts is a special case of dividing a segment in this respect. The two-handed saw works in the most democratic way, and each neighbor at the desk gets the same stick:
At this solemn hour the drums beat, welcoming the significant proportion. And general formulas ![]() miraculously transformed into something familiar and simple:
miraculously transformed into something familiar and simple: ![]()
A convenient point is the fact that the coordinates of the ends of the segment can be rearranged painlessly: ![]()
In general formulas, such a luxurious room, as you understand, does not work. And here there is no particular need for it, so it’s a nice little thing.
For the spatial case, an obvious analogy holds. If the ends of a segment are given, then the coordinates of its midpoint are expressed by the formulas:
Example 7
A parallelogram is defined by the coordinates of its vertices. Find the point of intersection of its diagonals.
Solution: Those who wish can complete the drawing. I especially recommend graffiti to those who have completely forgotten their school geometry course.
According to the well-known property, the diagonals of a parallelogram are divided in half by their point of intersection, so the problem can be solved in two ways.
Method one: Consider opposite vertices ![]() . Using the formulas for dividing a segment in half, we find the middle of the diagonal:
. Using the formulas for dividing a segment in half, we find the middle of the diagonal: