Angka keenam dalam deret Fibonacci. Angka Fibonacci: fakta matematika yang menarik

Pernahkah Anda mendengar bahwa matematika disebut sebagai “ratu segala ilmu”? Apakah Anda setuju dengan pernyataan ini? Selama matematika tetap menjadi kumpulan soal membosankan di buku teks bagi Anda, Anda hampir tidak dapat merasakan keindahan, keserbagunaan, dan bahkan humor dari ilmu ini.

Namun ada topik dalam matematika yang membantu melakukan observasi menarik tentang hal-hal dan fenomena yang umum bagi kita. Dan bahkan mencoba menembus tabir misteri penciptaan Alam Semesta kita. Ada pola menarik di dunia yang dapat dijelaskan dengan menggunakan matematika.

Memperkenalkan angka Fibonacci

Angka Fibonacci sebutkan unsur-unsur barisan bilangan. Di dalamnya, setiap angka berikutnya dalam suatu rangkaian diperoleh dengan menjumlahkan dua angka sebelumnya.

Contoh barisan: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987…

Anda dapat menulisnya seperti ini:

F 0 = 0, F 1 = 1, F n = F n-1 + F n-2, n ≥ 2

Anda dapat memulai rangkaian angka Fibonacci dengan nilai negatif N. Selain itu, barisan dalam hal ini bersifat dua arah (yaitu mencakup bilangan negatif dan positif) dan cenderung tak terhingga pada kedua arah.

Contoh barisan tersebut: -55, -34, -21, -13, -8, 5, 3, 2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21 , 34, 55.

Rumusnya dalam hal ini terlihat seperti ini:

F n = F n+1 - F n+2 atau Anda dapat melakukan ini: F -n = (-1) n+1 Fn.

Apa yang sekarang kita kenal sebagai “bilangan Fibonacci” telah dikenal oleh ahli matematika India kuno jauh sebelum angka tersebut mulai digunakan di Eropa. Dan nama ini umumnya merupakan salah satu anekdot sejarah yang berkesinambungan. Mari kita mulai dengan fakta bahwa Fibonacci sendiri tidak pernah menyebut dirinya Fibonacci selama hidupnya - nama ini mulai diterapkan pada Leonardo dari Pisa hanya beberapa abad setelah kematiannya. Tapi mari kita bicarakan semuanya secara berurutan.

Leonardo dari Pisa alias Fibonacci

Putra seorang saudagar yang menjadi ahli matematika, dan kemudian mendapat pengakuan dari anak cucu sebagai ahli matematika besar pertama di Eropa pada Abad Pertengahan. Paling tidak berkat angka Fibonacci (yang, mari kita ingat, belum disebut demikian). Yang ia gambarkan pada awal abad ke-13 dalam karyanya “Liber abaci” (“Book of Abacus”, 1202).

Saya bepergian dengan ayah saya ke Timur, Leonardo belajar matematika dengan guru-guru Arab (dan pada masa itu mereka termasuk spesialis terbaik dalam bidang ini, dan dalam banyak ilmu lainnya). Ia membaca karya-karya matematikawan Purbakala dan India Kuno dalam terjemahan bahasa Arab.

Setelah benar-benar memahami semua yang telah dibacanya dan menggunakan pikiran ingin tahunya, Fibonacci menulis beberapa risalah ilmiah tentang matematika, termasuk “Kitab Sempoa” yang disebutkan di atas. Selain itu saya membuat:

"Practica geometriae" ("Praktik Geometri", 1220);
"Flos" ("Bunga", 1225 - studi tentang persamaan kubik);
"Liber quadratorum" ("Book of Squares", 1225 - soal persamaan kuadrat tak tentu).

Ia adalah penggemar berat turnamen matematika, sehingga dalam risalahnya ia menaruh banyak perhatian pada analisis berbagai masalah matematika.

Hanya ada sedikit informasi biografi yang tersisa tentang kehidupan Leonardo. Adapun nama Fibonacci, di mana ia memasuki sejarah matematika, baru diberikan kepadanya pada abad ke-19.

Fibonacci dan permasalahannya

Setelah Fibonacci, masih ada sejumlah besar soal yang sangat populer di kalangan matematikawan pada abad-abad berikutnya. Kita akan melihat soal kelinci, yang diselesaikan dengan menggunakan bilangan Fibonacci.

Kelinci bukan hanya bulunya yang berharga

Fibonacci menetapkan kondisi berikut: terdapat sepasang kelinci yang baru lahir (jantan dan betina) dari jenis yang menarik sehingga mereka secara teratur (mulai dari bulan kedua) menghasilkan keturunan - selalu sepasang kelinci baru. Juga, seperti yang Anda duga, laki-laki dan perempuan.

Kelinci bersyarat ini ditempatkan di ruang terbatas dan berkembang biak dengan penuh semangat. Ditetapkan juga bahwa tidak ada satu pun kelinci yang mati karena penyakit kelinci yang misterius.

Kita perlu menghitung berapa banyak kelinci yang akan kita dapatkan dalam setahun.

Awal 1 bulan kita mempunyai 1 pasang kelinci. Di akhir bulan mereka kawin.
Bulan kedua - kita sudah mempunyai 2 pasang kelinci (sepasang mempunyai induk + 1 pasang adalah keturunannya).
Bulan ketiga: Pasangan pertama melahirkan pasangan baru, pasangan kedua kawin. Total - 3 pasang kelinci.
Bulan keempat : Pasangan pertama melahirkan pasangan baru, pasangan kedua tidak menyia-nyiakan waktu dan juga melahirkan pasangan baru, pasangan ketiga masih hanya kawin. Total - 5 pasang kelinci.

Jumlah kelinci yang masuk N bulan ke- = banyaknya pasang kelinci bulan sebelumnya + banyaknya pasang kelinci yang baru lahir (jumlah pasang kelinci sama dengan jumlah pasang kelinci 2 bulan sebelumnya). Dan semua itu dijelaskan dengan rumus yang telah kami berikan di atas: F n = F n-1 + F n-2.

Dengan demikian, kita memperoleh penjelasan berulang (tentang pengulangan– di bawah) urutan nomor. Di mana setiap angka berikutnya sama dengan jumlah dua angka sebelumnya:

1 + 1 = 2
2 + 1 = 3
3 + 2 = 5
5 + 3 = 8
8 + 5 = 13
13 + 8 = 21
21 + 13 = 34
34 + 21 = 55
55 + 34 = 89
89 + 55 = 144
144 + 89 = 233
233+ 144 = 377 <…>

Anda dapat melanjutkan urutannya untuk waktu yang lama: 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987<…>. Namun karena kami telah menetapkan jangka waktu tertentu - satu tahun, kami tertarik dengan hasil yang diperoleh pada "langkah" ke-12. Itu. Anggota urutan ke-13: 377.

Jawaban dari soal: Akan didapat 377 ekor kelinci jika semua syarat terpenuhi.

Salah satu sifat barisan bilangan Fibonacci yang sangat menarik. Jika Anda mengambil dua pasangan berurutan dari suatu rangkaian dan membagi bilangan yang lebih besar dengan bilangan yang lebih kecil, hasilnya akan semakin dekat rasio emas(Anda dapat membaca lebih lanjut tentangnya nanti di artikel).

Dalam istilah matematika, "batas hubungan sebuah n+1 Ke sebuah sama dengan rasio emas".

Lebih banyak masalah teori bilangan

Carilah bilangan yang habis dibagi 7. Selain itu, jika dibagi dengan 2, 3, 4, 5, 6, maka sisanya adalah satu.
Temukan bilangan kuadratnya. Diketahui bahwa jika Anda menambahkan 5 atau mengurangi 5, Anda kembali mendapatkan bilangan kuadrat.

Kami menyarankan Anda mencari sendiri jawaban atas masalah ini. Anda dapat meninggalkan kami pilihan Anda di komentar artikel ini. Dan kemudian kami akan memberi tahu Anda apakah perhitungan Anda benar.

Penjelasan tentang rekursi

Pengulangan– definisi, deskripsi, gambaran suatu objek atau proses yang memuat objek atau proses itu sendiri. Artinya, suatu objek atau proses pada hakikatnya adalah bagian dari dirinya sendiri.

Rekursi banyak digunakan dalam matematika dan ilmu komputer, dan bahkan dalam seni dan budaya populer.

Angka Fibonacci ditentukan menggunakan relasi perulangan. Untuk nomor n>2 n- nomor e sama (n – 1) + (n – 2).

Penjelasan tentang rasio emas

Rasio emas- membagi keseluruhan (misalnya, segmen) menjadi bagian-bagian yang terkait menurut prinsip berikut: bagian yang lebih besar berhubungan dengan yang lebih kecil dengan cara yang sama seperti nilai keseluruhan (misalnya, jumlah dua segmen) adalah ke bagian yang lebih besar.

Penyebutan pertama tentang rasio emas dapat ditemukan di Euclid dalam risalahnya “Elements” (sekitar 300 SM). Dalam konteks membuat persegi panjang beraturan.

Istilah yang kita kenal mulai beredar pada tahun 1835 oleh ahli matematika Jerman Martin Ohm.

Jika kita menggambarkan rasio emas secara kasar, maka ini mewakili pembagian proporsional menjadi dua bagian yang tidak sama: sekitar 62% dan 38%. Dalam istilah numerik, rasio emas adalah angka 1,6180339887 .

Rasio emas menemukan penerapan praktis dalam seni rupa (lukisan karya Leonardo da Vinci dan pelukis Renaisans lainnya), arsitektur, sinema (“Battleship Potemkin” oleh S. Esenstein) dan bidang lainnya. Sejak lama diyakini bahwa rasio emas adalah proporsi yang paling estetis. Pendapat ini masih populer hingga saat ini. Meski menurut hasil penelitian, secara visual kebanyakan orang tidak menganggap proporsi ini sebagai pilihan yang paling berhasil dan menganggapnya terlalu memanjang (tidak proporsional).

Panjang bagian Dengan = 1, A = 0,618, B = 0,382.
Sikap Dengan Ke A = 1, 618.
Sikap Dengan Ke B = 2,618

Sekarang mari kita kembali ke angka Fibonacci. Mari kita ambil dua suku berurutan dari barisannya. Bagilah angka yang lebih besar dengan angka yang lebih kecil dan dapatkan kira-kira 1,618. Dan sekarang kita menggunakan bilangan yang sama lebih besar dan anggota deret berikutnya (yaitu bilangan yang lebih besar) - rasionya awal 0,618.

Berikut contohnya: 144, 233, 377.

233/144 = 1,618 dan 233/377 = 0,618

Omong-omong, jika Anda mencoba melakukan eksperimen yang sama dengan angka-angka dari awal barisan (misalnya, 2, 3, 5), tidak ada yang akan berhasil. Hampir. Aturan rasio emas hampir tidak diikuti untuk awal rangkaian. Namun saat Anda menelusuri seri dan jumlahnya bertambah, ini berfungsi dengan baik.

Dan untuk menghitung seluruh rangkaian bilangan Fibonacci, cukup mengetahui tiga suku barisan tersebut, yang muncul satu demi satu. Anda dapat melihatnya sendiri!

Persegi Panjang Emas dan Spiral Fibonacci

Paralel menarik lainnya antara angka Fibonacci dan rasio emas adalah apa yang disebut “persegi panjang emas”: sisi-sisinya memiliki perbandingan 1,618 banding 1. Tapi kita sudah tahu apa itu angka 1,618 bukan?

Misalnya, ambil dua suku berurutan dari deret Fibonacci - 8 dan 13 - dan buatlah sebuah persegi panjang dengan parameter berikut: lebar = 8, panjang = 13.

Dan kemudian kita akan membagi persegi panjang besar menjadi yang lebih kecil. Syarat wajib: panjang sisi persegi panjang harus sesuai dengan bilangan Fibonacci. Itu. Panjang sisi persegi panjang yang lebih besar harus sama dengan jumlah sisi dua persegi panjang yang lebih kecil.

Caranya dilakukan pada gambar ini (untuk memudahkan, gambar ditandatangani dengan huruf latin).

Omong-omong, Anda bisa membuat persegi panjang dalam urutan terbalik. Itu. mulailah membangun dengan kotak dengan sisi 1. Yang mana, dengan berpedoman pada prinsip yang disebutkan di atas, gambar dengan sisi yang sama dengan angka Fibonacci diselesaikan. Secara teoritis, hal ini dapat dilanjutkan tanpa batas waktu - lagipula, deret Fibonacci secara formal tidak terbatas.

Jika kita menghubungkan sudut-sudut persegi panjang yang diperoleh pada gambar dengan garis halus, kita mendapatkan spiral logaritmik. Atau lebih tepatnya, kasus khususnya adalah spiral Fibonacci. Hal ini ditandai dengan, khususnya, oleh kenyataan bahwa ia tidak memiliki batas dan tidak berubah bentuk.

Spiral serupa sering ditemukan di alam. Cangkang kerang adalah salah satu contoh yang paling mencolok. Apalagi beberapa galaksi yang terlihat dari Bumi berbentuk spiral. Jika Anda memperhatikan ramalan cuaca di TV, Anda mungkin memperhatikan bahwa siklon memiliki bentuk spiral yang serupa jika difoto dari satelit.

Sangat mengherankan bahwa heliks DNA juga mematuhi aturan bagian emas - pola yang sesuai dapat dilihat pada interval tikungannya.

“Kebetulan” yang menakjubkan seperti itu pasti menggairahkan pikiran dan memunculkan pembicaraan tentang suatu algoritma tunggal yang dipatuhi oleh semua fenomena dalam kehidupan Semesta. Sekarang apakah Anda mengerti mengapa artikel ini disebut demikian? Dan dunia menakjubkan seperti apa yang bisa dibukakan matematika untuk Anda?

Angka Fibonacci di alam

Hubungan antara angka Fibonacci dan rasio emas menunjukkan pola yang menarik. Sangat penasaran sehingga tergoda untuk mencoba menemukan barisan yang mirip dengan bilangan Fibonacci di alam dan bahkan pada peristiwa sejarah. Dan alam memang memunculkan asumsi seperti itu. Namun bisakah segala sesuatu dalam hidup kita dijelaskan dan dideskripsikan menggunakan matematika?

Contoh makhluk hidup yang dapat dijelaskan dengan menggunakan deret Fibonacci:

susunan daun (dan cabang) pada tumbuhan - jarak antara keduanya berkorelasi dengan bilangan Fibonacci (phyllotaxis);

susunan biji bunga matahari (biji disusun dalam dua baris spiral yang dipilin ke arah yang berbeda: satu baris searah jarum jam, yang lainnya berlawanan arah jarum jam);

susunan sisik kerucut pinus;
kelopak bunga;
sel nanas;
rasio panjang ruas jari tangan manusia (kurang-lebih), dll.

Masalah kombinatorik

Bilangan Fibonacci banyak digunakan dalam menyelesaikan masalah kombinatorik.

Kombinatorik adalah cabang matematika yang mempelajari pemilihan sejumlah elemen tertentu dari himpunan yang ditentukan, pencacahan, dll.

Mari kita lihat contoh soal kombinatorik yang dirancang untuk tingkat sekolah menengah (sumber - http://www.problems.ru/).

Tugas 1:

Lesha menaiki tangga 10 langkah. Pada suatu waktu dia melompat satu atau dua langkah. Berapa banyak cara Lesha menaiki tangga tersebut?

Banyaknya cara Lesha menaiki tangga N langkah-langkah, mari kita tunjukkan dan N. Oleh karena itu sebuah 1 = 1, sebuah 2= 2 (lagipula, Lesha melompat satu atau dua langkah).

Disepakati juga bahwa Lesha melompati tangga n> 2 Langkah. Katakanlah dia melompat dua langkah untuk pertama kalinya. Artinya, sesuai dengan kondisi soal, ia perlu melompati soal lain n – 2 Langkah. Maka banyaknya cara untuk menyelesaikan pendakian dijelaskan sebagai sebuah n–2. Dan jika kita asumsikan pertama kali Lesha melompat hanya satu langkah, maka kita uraikan banyak cara untuk menyelesaikan pendakian sebagai sebuah n–1.

Dari sini kita mendapatkan persamaan berikut: an = an–1 + an–2(terlihat familier, bukan?).

Sejak kita tahu sebuah 1 Dan sebuah 2 dan ingat sesuai kondisi soal ada 10 langkah, hitung semua urut dan N: sebuah 3 = 3, sebuah 4 = 5, sebuah 5 = 8, sebuah 6 = 13, sebuah 7 = 21, sebuah 8 = 34, sebuah 9 = 55, sebuah 10 = 89.

Jawaban: 89 cara.

Tugas #2:

Anda perlu mencari banyaknya kata yang panjangnya 10 huruf yang hanya terdiri dari huruf “a” dan “b” dan tidak boleh mengandung dua huruf “b” berturut-turut.

Mari kita nyatakan dengan sebuah panjang jumlah kata N huruf yang hanya terdiri dari huruf “a” dan “b” serta tidak memuat dua huruf “b” yang berurutan. Cara, sebuah 1= 2, sebuah 2= 3.

Berurutan sebuah 1, sebuah 2, <…>, sebuah kami akan mengekspresikan setiap anggota berikutnya melalui yang sebelumnya. Oleh karena itu, banyaknya kata yang panjangnya adalah N huruf yang juga tidak mengandung huruf ganda “b” dan diawali dengan huruf “a” adalah sebuah n–1. Dan jika kata-katanya panjang N huruf diawali dengan huruf “b”, maka logis jika huruf berikutnya pada kata tersebut adalah “a” (toh, tidak mungkin ada dua “b” sesuai dengan kondisi soal). Oleh karena itu, banyaknya kata yang panjangnya adalah N dalam hal ini kami menyatakan huruf sebagai sebuah n–2. Dalam kasus pertama dan kedua, kata apa pun (panjangnya n – 1 Dan n – 2 huruf masing-masing) tanpa ganda “b”.

Kami dapat menjelaskan alasannya an = an–1 + an–2.

Sekarang mari kita hitung sebuah 3= sebuah 2+ sebuah 1= 3 + 2 = 5, sebuah 4= sebuah 3+ sebuah 2= 5 + 3 = 8, <…>, sebuah 10= sebuah 9+ sebuah 8= 144. Dan kita mendapatkan deret Fibonacci yang familiar.

Jawaban: 144.

Tugas #3:

Bayangkan ada pita yang dibagi menjadi beberapa sel. Itu mengarah ke kanan dan berlangsung tanpa batas waktu. Tempatkan belalang di kotak pertama rekaman itu. Di sel mana pun dia berada, dia hanya bisa bergerak ke kanan: satu sel, atau dua. Berapa banyak cara yang dapat dilakukan belalang untuk melompat dari awal rekaman ke N-sel ke-?

Mari kita nyatakan banyak cara memindahkan belalang di sepanjang sabuk ke N-sel seperti sebuah. Pada kasus ini sebuah 1 = sebuah 2= 1. Juga masuk n+1 Belalang dapat masuk ke sel ke - dari mana saja N-sel, atau dengan melompati sel tersebut. Dari sini sebuah n + 1 = sebuah – 1 + sebuah. Di mana sebuah = Fn – 1.

Menjawab: Fn – 1.

Anda dapat membuat sendiri soal serupa dan mencoba menyelesaikannya dalam pelajaran matematika bersama teman sekelas Anda.

Angka Fibonacci dalam budaya populer

Tentu saja, fenomena yang tidak biasa seperti angka Fibonacci menarik perhatian. Masih ada sesuatu yang menarik dan bahkan misterius dalam pola yang diverifikasi secara ketat ini. Tidak mengherankan jika deret Fibonacci entah bagaimana “menyala” dalam banyak karya budaya populer modern dari berbagai genre.

Kami akan memberi tahu Anda tentang beberapa di antaranya. Dan Anda mencoba mencari diri Anda lagi. Jika Anda menemukannya, bagikan kepada kami di komentar – kami juga penasaran!

Angka Fibonacci disebutkan dalam buku terlaris Dan Brown The Da Vinci Code: deret Fibonacci berfungsi sebagai kode yang digunakan oleh karakter utama buku untuk membuka brankas.
Dalam film Amerika tahun 2009 Mr. Nothing, dalam satu episode alamat sebuah rumah merupakan bagian dari deret Fibonacci - 12358. Selain itu, di episode lain tokoh utama harus menghubungi nomor telepon yang intinya sama, namun sedikit terdistorsi. (digit tambahan setelah angka 5) Urutan : 123-581-1321.
Dalam serial “Connection” tahun 2012, tokoh utama, seorang anak laki-laki penderita autisme, mampu melihat pola peristiwa yang terjadi di dunia. Termasuk melalui angka Fibonacci. Dan kelola peristiwa ini juga melalui angka.
Pengembang game java untuk ponsel Doom RPG menempatkan pintu rahasia di salah satu level. Kode yang membukanya adalah deret Fibonacci.
Pada tahun 2012, band rock Rusia Splin merilis album konsep “Optical Deception.” Jalur kedelapan disebut “Fibonacci”. Syair pemimpin kelompok Alexander Vasiliev dimainkan pada deret angka Fibonacci. Untuk masing-masing sembilan suku berurutan terdapat jumlah baris yang bersesuaian (0, 1, 1, 2, 3, 5, 8, 13, 21):

0 Kereta berangkat

1 Salah satu sendi patah

1 Satu lengannya bergetar

2 Itu dia, ambil barangnya

Itu dia, ambil barangnya

3 Minta air mendidih

Kereta pergi ke sungai

Kereta melewati taiga<…>.

Limerick (puisi pendek dengan bentuk tertentu - biasanya lima baris, dengan skema rima tertentu, isinya lucu, di mana baris pertama dan terakhir diulang atau sebagian saling menduplikasi) oleh James Lyndon juga menggunakan referensi ke Fibonacci urutan sebagai motif lucu:

Makanan padat istri Fibonacci

Itu hanya untuk kepentingan mereka, tidak ada yang lain.

Para istri menimbang, menurut rumor,

Masing-masing seperti dua sebelumnya.

Mari kita simpulkan

Kami berharap hari ini kami dapat memberi tahu Anda banyak hal menarik dan bermanfaat. Misalnya, kini Anda bisa mencari spiral Fibonacci di alam sekitar Anda. Mungkin Andalah yang mampu mengungkap “rahasia kehidupan, alam semesta, dan secara umum”.

Gunakan rumus bilangan Fibonacci saat menyelesaikan soal kombinatorik. Anda dapat mengandalkan contoh yang dijelaskan dalam artikel ini.

blog.site, apabila menyalin materi seluruhnya atau sebagian, diperlukan link ke sumber aslinya.

Jangan sampai hilang. Berlangganan dan terima tautan ke artikel di email Anda.

Anda tentu akrab dengan gagasan bahwa matematika adalah ilmu terpenting dari semua ilmu pengetahuan. Namun banyak yang mungkin tidak setuju dengan hal ini, karena... terkadang matematika terkesan hanya sekedar soal, contoh, dan hal-hal membosankan serupa. Namun, matematika dapat dengan mudah menunjukkan kepada kita hal-hal yang familiar dari sisi yang sama sekali asing. Apalagi dia bahkan bisa mengungkap rahasia alam semesta. Bagaimana? Mari kita lihat angka Fibonacci.

Apa itu bilangan Fibonacci?

Bilangan Fibonacci merupakan unsur barisan bilangan yang setiap bilangan berikutnya dijumlahkan dengan dua bilangan sebelumnya, contoh: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89... Biasanya barisan seperti itu ditulis dengan rumus: F 0 = 0, F 1 = 1, F n = F n-1 + F n-2, n ≥ 2.

Bilangan Fibonacci dapat dimulai dengan nilai negatif "n", tetapi dalam kasus ini barisannya akan dua arah - bilangan tersebut akan mencakup bilangan positif dan negatif, cenderung tak terhingga di kedua arah. Contoh barisan tersebut adalah: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13 , 21, 34, dan rumusnya adalah: F n = F n+1 - F n+2 atau F -n = (-1) n+1 Fn.

Pencipta angka Fibonacci adalah salah satu ahli matematika pertama di Eropa pada Abad Pertengahan bernama Leonardo dari Pisa, yang sebenarnya dikenal sebagai Fibonacci - ia menerima julukan ini bertahun-tahun setelah kematiannya.

Semasa hidupnya, Leonardo dari Pisa sangat menyukai turnamen matematika, itulah sebabnya dalam karyanya (“Liber abaci” / “Book of Abacus”, 1202; “Practica geometriae” / “Practice of Geometry”, 1220, “Flos” / “Bunga”, 1225) - studi tentang persamaan kubik dan "Liber quadratorum" / "Book of Squares", 1225 - soal tentang persamaan kuadrat tak tentu) sangat sering menganalisis semua jenis masalah matematika.

Sangat sedikit yang diketahui tentang jalur kehidupan Fibonacci sendiri. Namun yang pasti adalah bahwa permasalahannya menikmati popularitas yang sangat besar di kalangan matematika pada abad-abad berikutnya. Kami akan mempertimbangkan salah satunya lebih lanjut.

Masalah Fibonacci dengan kelinci

Untuk menyelesaikan tugas tersebut, penulis menetapkan kondisi berikut: ada sepasang kelinci yang baru lahir (betina dan jantan), dibedakan berdasarkan ciri yang menarik - mulai bulan kedua kehidupan, mereka menghasilkan sepasang kelinci baru - juga betina dan seorang laki-laki. Kelinci dipelihara di ruang terbatas dan terus berkembang biak. Dan tidak ada seekor kelinci pun yang mati.

Tugas: menentukan jumlah kelinci dalam setahun.

Larutan:

Kita punya:

Sepasang kelinci di awal bulan pertama, yang kawin di akhir bulan
Dua pasang kelinci pada bulan kedua (pasangan pertama dan keturunannya)
Tiga pasang kelinci pada bulan ketiga (pasangan pertama, keturunan pasangan pertama bulan sebelumnya dan keturunan baru)
Lima pasang kelinci pada bulan keempat (pasangan pertama, keturunan pertama dan kedua dari pasangan pertama, keturunan ketiga dari pasangan pertama, dan keturunan pertama dari pasangan kedua)

Jumlah kelinci per bulan “n” = jumlah kelinci bulan lalu + jumlah pasangan kelinci baru, dengan kata lain rumus di atas: F n = F n-1 + F n-2. Hal ini menghasilkan barisan bilangan yang berulang (kita akan membicarakan rekursi nanti), dimana setiap bilangan baru sesuai dengan jumlah dari dua bilangan sebelumnya:

1 bulan: 1 + 1 = 2

2 bulan: 2 + 1 = 3

3 bulan: 3 + 2 = 5

4 bulan: 5 + 3 = 8

5 bulan: 8 + 5 = 13

6 bulan: 13 + 8 = 21

Bulan ke-7: 21 + 13 = 34

Bulan ke-8: 34 + 21 = 55

9 bulan: 55 + 34 = 89

Bulan ke 10: 89 + 55 = 144

Bulan ke-11: 144 + 89 = 233

12 bulan: 233+ 144 = 377

Dan rangkaian ini bisa berlanjut tanpa batas waktu, namun mengingat tugasnya adalah mencari jumlah kelinci setelah satu tahun, maka hasilnya adalah 377 pasang.

Penting juga untuk dicatat di sini bahwa salah satu sifat angka Fibonacci adalah jika Anda membandingkan dua pasangan berturut-turut dan kemudian membagi yang lebih besar dengan yang lebih kecil, hasilnya akan bergerak menuju rasio emas, yang juga akan kita bahas di bawah. .

Sementara itu, kami menawarkan kepada Anda dua soal lagi tentang bilangan Fibonacci:

Tentukan suatu bilangan kuadrat, yang hanya kita ketahui bahwa jika kita mengurangkan 5 atau menambahkan 5 ke bilangan tersebut, kita akan mendapatkan bilangan kuadrat lagi.
Tentukan suatu bilangan yang habis dibagi 7, namun dengan syarat membaginya dengan 2, 3, 4, 5 atau 6 menyisakan sisa 1.

Tugas-tugas seperti itu tidak hanya akan menjadi cara terbaik untuk mengembangkan pikiran, tetapi juga hiburan yang menghibur. Anda juga dapat mengetahui bagaimana masalah ini diselesaikan dengan mencari informasi di Internet. Kami tidak akan fokus pada mereka, tetapi akan melanjutkan cerita kami.

Apa itu rekursi dan rasio emas?

Pengulangan

Rekursi adalah deskripsi, definisi, atau gambaran suatu objek atau proses, yang berisi objek atau proses itu sendiri. Dengan kata lain, suatu objek atau proses dapat disebut sebagai bagian dari dirinya sendiri.

Rekursi banyak digunakan tidak hanya dalam ilmu matematika, tetapi juga dalam ilmu komputer, budaya populer, dan seni. Berlaku untuk bilangan Fibonacci, kita dapat mengatakan bahwa jika bilangan tersebut “n>2”, maka “n” = (n-1)+(n-2).

Rasio emas

Rasio emas adalah pembagian keseluruhan menjadi bagian-bagian yang berhubungan menurut prinsip: yang lebih besar berhubungan dengan yang lebih kecil dengan cara yang sama seperti nilai total berhubungan dengan bagian yang lebih besar.

Rasio emas pertama kali disebutkan oleh Euclid (dalam risalah “Elements,” sekitar 300 SM), berbicara tentang konstruksi persegi panjang beraturan. Namun, konsep yang lebih familiar diperkenalkan oleh matematikawan Jerman Martin Ohm.

Kira-kira rasio emas dapat direpresentasikan sebagai pembagian proporsional menjadi dua bagian yang berbeda, misalnya 38% dan 68%. Ekspresi numerik dari rasio emas adalah sekitar 1,6180339887.

Dalam prakteknya, rasio emas digunakan dalam arsitektur, seni rupa (lihat karya), bioskop dan bidang lainnya. Untuk waktu yang lama, seperti sekarang, rasio emas dianggap sebagai proporsi estetika, meskipun kebanyakan orang menganggapnya tidak proporsional - memanjang.

Anda dapat mencoba memperkirakan sendiri rasio emas, dengan dipandu oleh proporsi berikut:

Panjang ruas a = 0,618
Panjang ruas b= 0,382
Panjang ruas c = 1
Rasio c dan a = 1,618
Rasio c dan b = 2,618

Sekarang mari kita terapkan rasio emas pada bilangan Fibonacci: kita mengambil dua suku yang berdekatan dari barisan tersebut dan membagi suku yang lebih besar dengan suku yang lebih kecil. Kami mendapatkan sekitar 1.618. Jika kita mengambil angka yang sama lebih besar dan membaginya dengan angka berikutnya yang lebih besar, kita mendapatkan kira-kira 0,618. Cobalah sendiri: “bermain” dengan angka 21 dan 34 atau yang lainnya. Jika kita melakukan percobaan ini dengan bilangan pertama deret Fibonacci, maka hasil seperti itu tidak akan ada lagi, karena rasio emas "tidak berfungsi" di awal urutan. Ngomong-ngomong, untuk menentukan semua angka Fibonacci, Anda hanya perlu mengetahui tiga angka pertama yang berurutan.

Dan sebagai kesimpulan, ada lebih banyak bahan untuk dipikirkan.

Persegi Panjang Emas dan Spiral Fibonacci

“Persegi Panjang Emas” adalah hubungan lain antara rasio emas dan bilangan Fibonacci, karena... rasio aspeknya adalah 1,618 banding 1 (ingat angka 1,618!).

Berikut contohnya: kita ambil dua buah bilangan deret fibonacci, misal 8 dan 13, lalu gambarlah sebuah persegi panjang dengan lebar 8 cm dan panjang 13 cm, selanjutnya kita bagi persegi panjang utama menjadi persegi-panjang kecil, tetapi persegi panjang tersebut panjang dan lebar harus sesuai dengan angka Fibonacci - panjang salah satu sisi persegi panjang besar harus sama dengan dua panjang sisi persegi kecil.

Setelah ini, kita menghubungkan sudut-sudut semua persegi panjang yang kita miliki dengan garis halus dan mendapatkan kasus khusus spiral logaritmik - spiral Fibonacci. Sifat utamanya adalah tidak adanya batas dan perubahan bentuk. Spiral seperti itu sering ditemukan di alam: contoh yang paling mencolok adalah cangkang moluska, siklon dalam citra satelit, dan bahkan sejumlah galaksi. Namun yang lebih menarik adalah DNA organisme hidup juga mengikuti aturan yang sama, karena ingatkah Anda bahwa ia memiliki bentuk spiral?

Hal ini dan banyak kebetulan “acak” lainnya bahkan hingga saat ini menggairahkan kesadaran para ilmuwan dan menunjukkan bahwa segala sesuatu di Alam Semesta tunduk pada satu algoritma, apalagi algoritma matematis. Dan ilmu ini menyembunyikan sejumlah besar rahasia dan misteri yang sangat membosankan.

Namun, bukan hanya itu yang bisa dilakukan dengan rasio emas. Jika kita membagi satu dengan 0,618, kita mendapatkan 1,618; jika kita mengkuadratkannya, kita mendapatkan 2,618; jika kita membaginya menjadi tiga, kita mendapatkan 4,236. Ini adalah rasio ekspansi Fibonacci. Satu-satunya angka yang hilang di sini adalah 3.236, yang diusulkan oleh John Murphy.

Apa pendapat para ahli tentang konsistensi?

Beberapa orang mungkin mengatakan bahwa angka-angka ini sudah familiar karena digunakan dalam program analisis teknis untuk menentukan besarnya koreksi dan perluasan. Selain itu, deret yang sama memainkan peran penting dalam teori gelombang Eliot. Itu adalah basis numeriknya.

Pakar kami Nikolay adalah manajer portofolio terbukti di perusahaan investasi Vostok.

— Nikolay, apakah menurut Anda kemunculan angka Fibonacci dan turunannya pada grafik berbagai instrumen adalah suatu kebetulan? Dan apakah mungkin untuk mengatakan: “Penerapan praktis deret Fibonacci” terjadi?
— Saya memiliki sikap buruk terhadap mistisisme. Dan terlebih lagi pada grafik bursa. Segala sesuatu mempunyai alasannya masing-masing. dalam buku “Fibonacci Levels” dia dengan indah menggambarkan di mana rasio emas muncul, sehingga dia tidak terkejut bahwa rasio emas muncul di grafik kutipan bursa saham. Namun sia-sia! Dalam banyak contoh yang diberikannya, angka Pi sering muncul. Namun entah kenapa tidak termasuk dalam rasio harga.
— Jadi Anda tidak percaya pada keefektifan prinsip gelombang Eliot?
- Tidak, bukan itu intinya. Prinsip gelombang adalah satu hal. Rasio numeriknya berbeda. Dan alasan kemunculannya di grafik harga adalah yang ketiga
— Menurut Anda, apa alasan munculnya rasio emas di grafik saham?
— Jawaban yang benar atas pertanyaan ini mungkin memberi Anda Hadiah Nobel Ekonomi. Untuk saat ini kita bisa menebak alasan sebenarnya. Mereka jelas tidak selaras dengan alam. Ada banyak model penetapan harga pertukaran. Mereka tidak menjelaskan fenomena yang dimaksud. Namun tidak memahami hakikat suatu fenomena tidak seharusnya mengingkari fenomena itu sendiri.
— Dan jika undang-undang ini dibuka, apakah akan mampu menghancurkan proses pertukaran?
— Seperti yang ditunjukkan oleh teori gelombang yang sama, hukum perubahan harga saham adalah murni psikologi. Bagi saya pengetahuan tentang undang-undang ini tidak akan mengubah apapun dan tidak akan mampu menghancurkan bursa.

Materi disediakan oleh blog webmaster Maxim.

Kebetulan prinsip-prinsip dasar matematika dalam berbagai teori nampaknya luar biasa. Mungkin itu fantasi atau disesuaikan dengan hasil akhirnya. Tunggu dan lihat. Banyak hal yang sebelumnya dianggap tidak biasa atau tidak mungkin dilakukan: eksplorasi ruang angkasa, misalnya, telah menjadi hal biasa dan tidak mengejutkan siapa pun. Selain itu, teori gelombang, yang mungkin tidak dapat dipahami, akan menjadi lebih mudah diakses dan dipahami seiring berjalannya waktu. Apa yang sebelumnya tidak diperlukan, di tangan seorang analis berpengalaman, akan menjadi alat yang ampuh untuk memprediksi perilaku di masa depan.

Angka Fibonacci di alam.

Lihat

Sekarang, mari kita bahas bagaimana Anda dapat menyangkal fakta bahwa deret digital Fibonacci terlibat dalam pola apa pun di alam.

Mari kita ambil dua angka lainnya dan buat barisan dengan logika yang sama dengan angka Fibonacci. Artinya, suku berikutnya dalam barisan tersebut sama dengan jumlah dua suku sebelumnya. Sebagai contoh, mari kita ambil dua angka: 6 dan 51. Sekarang kita akan membuat barisan yang akan kita selesaikan dengan dua angka 1860 dan 3009. Perhatikan bahwa ketika membagi angka-angka ini, kita mendapatkan angka yang mendekati rasio emas.

Pada saat yang sama, angka-angka yang diperoleh dengan membagi pasangan lain berkurang dari yang pertama ke yang terakhir, yang memungkinkan kita untuk mengatakan bahwa jika deret ini berlanjut tanpa batas waktu, maka kita akan mendapatkan angka yang sama dengan rasio emas.

Jadi, angka Fibonacci sama sekali tidak menonjol. Ada barisan bilangan lain, yang jumlahnya tak terhingga, yang sebagai hasil operasi yang sama menghasilkan bilangan emas phi.

Fibonacci bukanlah seorang esoteris. Dia tidak ingin memasukkan mistisisme apa pun ke dalam angka-angka itu, dia hanya memecahkan masalah biasa tentang kelinci. Dan dia menuliskan urutan angka yang mengikuti masalahnya, pada bulan pertama, kedua dan bulan lainnya, berapa jumlah kelinci setelah dikawinkan. Dalam setahun, dia menerima urutan yang sama. Dan aku tidak menjalin hubungan. Tidak ada pembicaraan tentang proporsi emas atau hubungan ketuhanan. Semua ini ditemukan setelah dia selama Renaisans.

Dibandingkan dengan matematika, kelebihan Fibonacci sangat besar. Ia mengadopsi sistem bilangan dari bangsa Arab dan membuktikan keabsahannya. Itu adalah perjuangan yang berat dan panjang. Dari sistem bilangan Romawi: berat dan tidak nyaman untuk dihitung. Itu menghilang setelah Revolusi Perancis. Fibonacci tidak ada hubungannya dengan rasio emas.

Teks karya diposting tanpa gambar dan rumus.
Versi lengkap karya ini tersedia di tab "File Kerja" dalam format PDF

Perkenalan

TUJUAN TERTINGGI MATEMATIKA ADALAH MENEMUKAN ORDERAN TERSEMBUNYI DALAM KEKACAUAN YANG DI SEKITAR KITA.

Viner N.

Seseorang berjuang untuk mendapatkan pengetahuan sepanjang hidupnya, mencoba mempelajari dunia di sekitarnya. Dan dalam proses observasi timbul pertanyaan-pertanyaan yang memerlukan jawaban. Jawabannya ditemukan, namun pertanyaan baru muncul. Dalam temuan arkeologis, dalam jejak-jejak peradaban, berjauhan dalam ruang dan waktu, ditemukan satu unsur yang sama - suatu pola berbentuk spiral. Beberapa menganggapnya sebagai simbol matahari dan mengasosiasikannya dengan Atlantis yang legendaris, namun arti sebenarnya tidak diketahui. Apa kesamaan bentuk galaksi dan siklon atmosfer, susunan daun pada batang, dan susunan biji pada bunga matahari? Pola-pola ini bermuara pada apa yang disebut spiral “emas”, deret Fibonacci menakjubkan yang ditemukan oleh ahli matematika besar Italia pada abad ke-13.

Sejarah angka Fibonacci

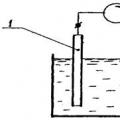
Pertama kali saya mendengar tentang apa itu bilangan Fibonacci dari seorang guru matematika. Tapi, selain itu, saya tidak tahu bagaimana urutan angka-angka ini muncul. Inilah yang sebenarnya membuat rangkaian ini terkenal, bagaimana pengaruhnya terhadap seseorang, saya ingin memberi tahu Anda. Sedikit yang diketahui tentang Leonardo Fibonacci. Bahkan tidak ada tanggal pasti lahirnya. Diketahui bahwa ia dilahirkan pada tahun 1170 dari sebuah keluarga pedagang di kota Pisa di Italia. Ayah Fibonacci sering mengunjungi Aljazair untuk urusan perdagangan, dan Leonardo belajar matematika di sana dengan guru-guru Arab. Selanjutnya, ia menulis beberapa karya matematika, yang paling terkenal adalah “Kitab Sempoa”, yang berisi hampir semua informasi aritmatika dan aljabar pada masa itu. 2

Bilangan Fibonacci merupakan barisan bilangan yang mempunyai sejumlah sifat. Fibonacci menemukan barisan bilangan ini secara tidak sengaja ketika dia mencoba memecahkan masalah praktis tentang kelinci pada tahun 1202. “Seseorang meletakkan sepasang kelinci di suatu tempat tertentu, dipagari tembok di semua sisinya, untuk mengetahui berapa pasang kelinci yang akan lahir sepanjang tahun, jika sifat kelinci sedemikian rupa sehingga setelah sebulan akan lahir sepasang. kelinci melahirkan sepasang lagi, dan kelinci melahirkan pada bulan kedua setelah kelahiranmu." Saat memecahkan masalah tersebut, ia memperhitungkan bahwa setiap pasang kelinci melahirkan dua pasang lagi sepanjang hidupnya, dan kemudian mati. Beginilah barisan bilangan yang muncul: 1, 1, 2, 3, 5, 8, 13, 21, ... Pada barisan ini, setiap bilangan berikutnya sama dengan jumlah dua bilangan sebelumnya. Itu disebut deret Fibonacci. Sifat matematika barisan tersebut

Saya ingin menjelajahi rangkaian ini, dan saya menemukan beberapa propertinya. Pola ini sangat penting. Deret tersebut perlahan-lahan mendekati rasio konstanta tertentu sekitar 1,618, dan rasio bilangan apa pun ke bilangan berikutnya kira-kira 0,618.

Anda dapat melihat sejumlah sifat menarik dari bilangan Fibonacci: dua bilangan bertetangga relatif prima; setiap bilangan ketiga adalah genap; setiap tanggal lima belas berakhir dengan nol; setiap yang keempat adalah kelipatan tiga. Jika Anda memilih 10 angka yang berdekatan dari deret Fibonacci dan menjumlahkannya, Anda akan selalu mendapatkan angka yang merupakan kelipatan 11. Tapi bukan itu saja. Setiap jumlah sama dengan angka 11 dikalikan suku ketujuh barisan tertentu. Inilah fitur menarik lainnya. Untuk sembarang n, jumlah n suku pertama barisan tersebut akan selalu sama dengan selisih antara suku ke-(n+ 2) dan suku pertama barisan tersebut. Fakta ini dapat dinyatakan dengan rumus: 1+1+2+3+5+…+an=an+2 - 1. Sekarang kita mempunyai trik berikut: mencari jumlah semua suku

barisan antara dua suku tertentu, cukup mencari selisih suku (n+2)-x yang bersesuaian. Misalnya, a 26 +…+a 40 = a 42 - a 27. Sekarang mari kita cari hubungan antara Fibonacci, Pythagoras dan “rasio emas”. Bukti paling terkenal dari kejeniusan matematika umat manusia adalah teorema Pythagoras: dalam segitiga siku-siku mana pun, kuadrat sisi miringnya sama dengan jumlah kuadrat kakinya: c 2 =b 2 +a 2. Dari sudut pandang geometri, kita dapat menganggap semua sisi segitiga siku-siku sebagai sisi-sisi dari tiga persegi yang dibangun di atasnya. Teorema Pythagoras menyatakan bahwa luas persegi yang dibangun pada sisi-sisi segitiga siku-siku sama dengan luas persegi yang dibangun pada sisi miringnya. Jika panjang sisi-sisi suatu segitiga siku-siku adalah bilangan bulat, maka ketiga bilangan tersebut membentuk kelompok tiga bilangan yang disebut kembar tiga Pythagoras. Dengan menggunakan deret Fibonacci Anda dapat menemukan kembar tiga tersebut. Mari kita ambil empat bilangan berurutan dari barisan tersebut, misalnya 2, 3, 5 dan 8, dan buatlah tiga bilangan lagi sebagai berikut: 1) hasil kali dua bilangan ekstrem: 2*8=16; 2) hasil kali ganda dari dua bilangan di tengah: 2* (3*5)=30;3) jumlah kuadrat dua bilangan rata-rata: 3 2 +5 2 =34; 34 2 =30 2 +16 2. Metode ini berlaku untuk empat angka Fibonacci yang berurutan. Tiga angka berurutan dalam deret Fibonacci berperilaku dapat diprediksi. Jika Anda mengalikan dua angka ekstrem dan membandingkan hasilnya dengan kuadrat angka rata-rata, hasilnya akan selalu berbeda satu. Misalnya untuk bilangan 5, 8 dan 13 kita peroleh: 5*13=8 2 +1. Jika Anda melihat properti ini dari sudut pandang geometris, Anda akan melihat sesuatu yang aneh. Bagilah persegi tersebut

berukuran 8x8 (total 64 kotak kecil) menjadi empat bagian, panjang sisinya sama dengan angka Fibonacci. Sekarang dari bagian ini kita akan membuat persegi panjang berukuran 5x13. Luasnya 65 kotak kecil. Dari mana datangnya kotak tambahan itu? Masalahnya adalah persegi panjang yang ideal tidak terbentuk, tetapi ada celah kecil yang tersisa, yang secara total memberikan satuan luas tambahan ini. Segitiga Pascal juga memiliki keterkaitan dengan deret Fibonacci. Anda hanya perlu menulis garis-garis segitiga Pascal satu di bawah yang lain, lalu menjumlahkan elemen-elemennya secara diagonal. Hasilnya adalah deret Fibonacci.

Sekarang perhatikan sebuah persegi panjang emas, yang salah satu sisinya 1,618 kali lebih panjang dari sisi lainnya. Sekilas, bagi kita ini mungkin tampak seperti persegi panjang biasa. Namun, mari kita lakukan percobaan sederhana dengan dua kartu bank biasa. Mari kita letakkan salah satunya secara horizontal dan yang lainnya secara vertikal sehingga sisi bawahnya berada pada garis yang sama. Jika kita menggambar garis diagonal pada peta horizontal dan memanjangkannya, kita akan melihat bahwa garis tersebut akan melewati sudut kanan atas peta vertikal - suatu kejutan yang menyenangkan. Mungkin ini kebetulan, atau mungkin persegi panjang dan bentuk geometris lainnya yang menggunakan “rasio emas” ini sangat enak dipandang. Apakah Leonardo da Vinci memikirkan rasio emas saat mengerjakan karyanya? Tampaknya hal ini tidak mungkin terjadi. Namun, dapat dikatakan bahwa ia sangat mementingkan hubungan antara estetika dan matematika.

Angka Fibonacci di alam

Keterkaitan rasio emas dengan keindahan bukan hanya soal persepsi manusia. Tampaknya alam sendiri telah memberikan peran khusus kepada F. Jika Anda menuliskan kotak secara berurutan ke dalam persegi panjang "emas", lalu menggambar busur di setiap kotak, Anda akan mendapatkan kurva anggun yang disebut spiral logaritmik. Ini sama sekali bukan keingintahuan matematis. 5

Sebaliknya, garis luar biasa ini sering ditemukan di dunia fisik: dari cangkang nautilus hingga lengan galaksi, dan dalam spiral kelopak bunga mawar yang sedang mekar. Hubungan antara rasio emas dan angka Fibonacci sangat banyak dan mengejutkan. Mari kita perhatikan bunga yang bentuknya sangat berbeda dari bunga mawar - bunga matahari berbiji. Hal pertama yang kita lihat adalah benih tersusun dalam dua jenis spiral: searah jarum jam dan berlawanan arah jarum jam. Jika kita menghitung spiral searah jarum jam, kita mendapatkan dua angka yang tampak biasa: 21 dan 34. Ini bukan satu-satunya contoh di mana angka Fibonacci dapat ditemukan dalam struktur tumbuhan.

Alam memberi kita banyak contoh susunan benda-benda homogen yang dijelaskan dengan bilangan Fibonacci. Dalam berbagai susunan spiral pada bagian-bagian kecil tumbuhan, dua famili spiral biasanya dapat dilihat. Di salah satu kelompok spiral ini melengkung searah jarum jam, sedangkan di kelompok lain spiral melengkung berlawanan arah jarum jam. Jumlah spiral dari satu jenis dan jenis lainnya sering kali merupakan bilangan Fibonacci yang berdekatan. Jadi, jika kita mengambil ranting pinus yang masih muda, mudah terlihat bahwa jarumnya membentuk dua spiral, dari kiri bawah ke kanan atas. Pada banyak kerucut, bijinya tersusun dalam tiga spiral, melingkari batang kerucut dengan lembut. Mereka tersusun dalam lima spiral, berkelok-kelok tajam ke arah yang berlawanan. Dalam kerucut besar dimungkinkan untuk mengamati 5 dan 8, dan bahkan 8 dan 13 spiral. Spiral Fibonacci juga terlihat jelas pada nanas: biasanya ada 8 dan 13 spiral.

Tunas sawi putih melontarkan dengan kuat ke luar angkasa, berhenti, melepaskan sehelai daun, tetapi kali ini lebih pendek dari yang pertama, kembali melontarkan ke luar angkasa, tetapi dengan kekuatan yang lebih kecil, melepaskan sehelai daun yang ukurannya lebih kecil lagi dan terlontar lagi. . Dorongan pertumbuhannya secara bertahap menurun sebanding dengan bagian “emas”. Untuk mengapresiasi besarnya peran angka Fibonacci, Anda hanya perlu melihat keindahan alam di sekitar kita. Angka Fibonacci dapat ditemukan dalam besaran

cabang pada batang setiap tanaman yang tumbuh dan jumlah kelopaknya.

Mari kita hitung kelopak beberapa bunga - iris dengan 3 kelopak, primrose dengan 5 kelopak, ragweed dengan 13 kelopak, bunga jagung dengan 34 kelopak, aster dengan 55 kelopak, dll. Apakah ini suatu kebetulan, atau memang hukum alam? Lihatlah batang dan bunga yarrow. Dengan demikian, deret Fibonacci total dapat dengan mudah menafsirkan pola manifestasi angka “Emas” yang terdapat di alam. Hukum-hukum ini berlaku terlepas dari kesadaran dan keinginan kita untuk menerimanya atau tidak. Pola simetri “emas” dimanifestasikan dalam transisi energi partikel elementer, dalam struktur beberapa senyawa kimia, dalam sistem planet dan kosmik, dalam struktur gen organisme hidup, dalam struktur organ individu manusia dan tubuh sebagai secara keseluruhan, dan juga memanifestasikan dirinya dalam bioritme dan fungsi otak serta persepsi visual.

Angka Fibonacci dalam arsitektur

“Rasio Emas” juga terbukti dalam banyak kreasi arsitektur luar biasa sepanjang sejarah manusia. Ternyata ahli matematika Yunani dan Mesir kuno mengetahui koefisien ini jauh sebelum Fibonacci dan menyebutnya sebagai “rasio emas”. Orang Yunani menggunakan prinsip “rasio emas” dalam pembangunan Parthenon, dan orang Mesir menggunakan Piramida Agung Giza. Kemajuan teknologi konstruksi dan perkembangan material baru membuka peluang baru bagi para arsitek abad kedua puluh. Frank Lloyd Wright dari Amerika adalah salah satu pendukung utama arsitektur organik. Sesaat sebelum kematiannya, ia merancang Museum Solomon Guggenheim di New York, yang berbentuk spiral terbalik, dan interior museum menyerupai cangkang nautilus. Arsitek Polandia-Israel Zvi Hecker juga menggunakan struktur spiral dalam desainnya untuk Sekolah Heinz Galinski di Berlin, yang selesai pada tahun 1995. Hecker memulai dengan ide tentang bunga matahari yang memiliki lingkaran pusat, dari mana

Semua elemen arsitektur berbeda. Bangunannya merupakan kombinasi

spiral ortogonal dan konsentris, melambangkan interaksi pengetahuan manusia yang terbatas dan kekacauan alam yang terkendali. Arsitekturnya meniru tanaman yang mengikuti pergerakan Matahari, sehingga ruang kelas mendapat penerangan sepanjang hari.

Di Quincy Park yang terletak di Cambridge, Massachusetts (AS), spiral “emas” sering ditemukan. Taman ini dirancang pada tahun 1997 oleh seniman David Phillips dan terletak di dekat Clay Mathematical Institute. Lembaga ini merupakan pusat penelitian matematika yang terkenal. Di Quincy Park, Anda dapat berjalan-jalan di antara spiral “emas” dan lengkungan logam, relief dua cangkang, dan batu dengan simbol akar kuadrat. Tanda itu berisi informasi tentang rasio “emas”. Bahkan parkir sepeda pun menggunakan simbol F.

Angka Fibonacci dalam psikologi

Dalam psikologi, telah dicatat titik balik, krisis, dan revolusi yang menandai transformasi struktur dan fungsi jiwa dalam jalur kehidupan seseorang. Jika seseorang berhasil mengatasi krisis-krisis tersebut, maka ia menjadi mampu memecahkan masalah-masalah kelas baru yang bahkan belum pernah terpikirkan sebelumnya.

Adanya perubahan mendasar memberikan alasan untuk mempertimbangkan waktu hidup sebagai faktor penentu dalam perkembangan kualitas spiritual. Bagaimanapun juga, alam tidak mengukur waktu dengan murah hati untuk kita, “tidak peduli berapa banyak waktunya, begitu banyak yang akan terjadi,” tetapi hanya cukup untuk mewujudkan proses pembangunan:

dalam struktur tubuh;

dalam perasaan, pemikiran dan keterampilan psikomotorik - sampai mereka memperolehnya harmoni diperlukan untuk kemunculan dan peluncuran mekanisme tersebut

kreativitas;

dalam struktur potensi energi manusia.

Perkembangan tubuh tidak bisa dihentikan: anak menjadi dewasa. Dengan mekanisme kreativitas, semuanya tidak sesederhana itu. Perkembangannya bisa dihentikan dan arahnya diubah.

Apakah ada peluang untuk mengejar waktu? Niscaya. Tetapi untuk ini, Anda perlu melakukan banyak pekerjaan pada diri Anda sendiri. Apa yang berkembang secara bebas, tentu saja, tidak memerlukan usaha khusus: anak berkembang dengan bebas dan tidak memperhatikan pekerjaan yang sangat besar ini, karena proses perkembangan bebas itu tercipta tanpa kekerasan terhadap diri sendiri.

Bagaimana makna perjalanan hidup dipahami dalam kesadaran sehari-hari? Rata-rata orang melihatnya seperti ini: di bawah ada kelahiran, di atas ada puncak kehidupan, dan kemudian semuanya berjalan menurun.

Orang bijak akan berkata: semuanya jauh lebih rumit. Dia membagi pendakian menjadi beberapa tahap: masa kanak-kanak, remaja, remaja... Mengapa demikian? Hanya sedikit yang mampu menjawab, meskipun semua orang yakin bahwa ini adalah tahapan kehidupan yang tertutup dan tidak terpisahkan.

Untuk mengetahui bagaimana mekanisme kreativitas berkembang, V.V. Klimenko menggunakan matematika, yaitu hukum bilangan Fibonacci dan proporsi “bagian emas” - hukum alam dan kehidupan manusia.

Angka Fibonacci membagi hidup kita menjadi beberapa tahap sesuai dengan jumlah tahun yang dijalani: 0 - awal hitungan mundur - anak lahir. Ia masih kekurangan tidak hanya keterampilan psikomotorik, berpikir, perasaan, imajinasi, tetapi juga potensi energi operasional. Dia adalah awal dari kehidupan baru, harmoni baru;

1 - anak telah menguasai berjalan dan menguasai lingkungan terdekatnya;

2 - memahami ucapan dan tindakan menggunakan instruksi verbal;

3 - bertindak melalui kata-kata, mengajukan pertanyaan;

5 - "usia rahmat" - keselarasan psikomotorik, ingatan, imajinasi dan perasaan, yang sudah memungkinkan anak untuk merangkul dunia dengan segala integritasnya;

8 - perasaan mengemuka. Mereka dilayani oleh imajinasi, dan pemikiran, melalui kekritisannya, ditujukan untuk mendukung keharmonisan kehidupan internal dan eksternal;

13 - mekanisme bakat mulai bekerja, yang bertujuan untuk mengubah materi yang diperoleh dalam proses pewarisan, mengembangkan bakatnya sendiri;

21 - mekanisme kreativitas telah mendekati keadaan harmonis dan upaya sedang dilakukan untuk melakukan karya berbakat;

34—keselarasan pemikiran, perasaan, imajinasi dan keterampilan psikomotorik: lahirlah kemampuan bekerja secara cerdik;

55 - pada usia ini, asalkan keharmonisan jiwa dan raga tetap terjaga, seseorang siap menjadi pencipta. Dan seterusnya…

Apa serif Angka Fibonacci? Mereka dapat diibaratkan seperti bendungan di sepanjang jalur kehidupan. Bendungan ini menunggu kita masing-masing. Pertama-tama, Anda harus mengatasi masing-masingnya, dan kemudian dengan sabar meningkatkan tingkat perkembangan Anda sampai suatu hari nanti itu berantakan, membuka jalan ke aliran bebas berikutnya.

Sekarang setelah kita memahami arti dari poin-poin penting perkembangan terkait usia ini, mari kita coba menguraikan bagaimana hal itu terjadi.

B1 tahun anak itu menguasai cara berjalan. Sebelumnya, dia mengalami dunia dengan bagian depan kepalanya. Kini dia mengenal dunia dengan tangannya—suatu keistimewaan manusia yang luar biasa. Hewan itu bergerak di ruang angkasa, dan dia, dengan belajar, menguasai ruang dan menguasai wilayah tempat dia tinggal.

2 tahun- memahami kata dan bertindak sesuai dengannya. Artinya:

anak mempelajari jumlah minimum kata - makna dan cara tindakan;

belum memisahkan diri dari lingkungan hidup dan menyatu menjadi satu kesatuan dengan lingkungan hidup,

oleh karena itu dia bertindak sesuai dengan instruksi orang lain. Di usia ini dia adalah orang yang paling patuh dan menyenangkan kepada orang tuanya. Dari pribadi yang sensual, seorang anak berubah menjadi pribadi yang kognitif.

3 tahun- tindakan menggunakan kata-kata sendiri. Pemisahan orang ini dari lingkungan telah terjadi - dan dia belajar menjadi orang yang bertindak mandiri. Dari sini dia:

dengan sengaja menentang lingkungan dan orang tua, guru taman kanak-kanak, dll;

mewujudkan kedaulatannya dan memperjuangkan kemerdekaan;

mencoba menundukkan orang-orang dekat dan terkenal sesuai keinginannya.

Bagi seorang anak, sebuah kata adalah sebuah tindakan. Di sinilah orang yang aktif dimulai.

5 tahun- “zaman kasih karunia.” Dia adalah personifikasi harmoni. Permainan, tarian, gerakan cekatan - semuanya dipenuhi dengan harmoni, yang coba dikuasai seseorang dengan kekuatannya sendiri. Perilaku psikomotorik yang harmonis membantu mewujudkan keadaan baru. Oleh karena itu, anak fokus pada aktivitas psikomotorik dan mengupayakan tindakan yang paling aktif.

Perwujudan hasil kerja kepekaan dilakukan melalui:

kemampuan untuk menampilkan lingkungan dan diri kita sendiri sebagai bagian dari dunia ini (kita mendengar, melihat, menyentuh, mencium, dll. - semua indera bekerja untuk proses ini);

kemampuan merancang dunia luar, termasuk diri sendiri

(penciptaan sifat kedua, hipotesis - lakukan ini dan itu besok, bangun mesin baru, selesaikan masalah), dengan kekuatan pemikiran kritis, perasaan dan imajinasi;

kemampuan untuk menciptakan produk aktivitas yang kedua, buatan manusia, (realisasi rencana, tindakan mental atau psikomotorik tertentu dengan objek dan proses tertentu).

Setelah 5 tahun, mekanisme imajinasi muncul dan mulai mendominasi mekanisme lainnya. Anak itu melakukan banyak pekerjaan, menciptakan gambar-gambar fantastis, dan hidup di dunia dongeng dan mitos. Imajinasi anak yang hipertrofi menimbulkan keterkejutan pada orang dewasa, karena imajinasinya tidak sesuai dengan kenyataan.

8 tahun— perasaan muncul ke permukaan dan standar perasaan seseorang (kognitif, moral, estetika) muncul ketika anak secara jelas:

mengevaluasi yang diketahui dan yang tidak diketahui;

membedakan moral dari maksiat, moral dari maksiat;

keindahan dari apa yang mengancam kehidupan, harmoni dari kekacauan.

13 tahun— mekanisme kreativitas mulai bekerja. Namun bukan berarti ia bekerja dengan kapasitas penuh. Salah satu elemen mekanisme muncul ke permukaan, dan elemen lainnya berkontribusi pada kerjanya. Jika dalam masa perkembangan zaman ini keharmonisan dipertahankan, yang hampir selalu membangun kembali strukturnya, maka pemuda tanpa susah payah akan mencapai bendungan berikutnya, tanpa disadari akan mengatasinya dan akan hidup di zaman revolusioner. Di usia yang revolusioner, seorang pemuda harus mengambil langkah maju yang baru: memisahkan diri dari masyarakat terdekat dan menjalani kehidupan dan aktivitas yang harmonis di dalamnya. Tidak semua orang bisa menyelesaikan masalah yang muncul di hadapan kita masing-masing.

21 tahun. Jika seorang revolusioner berhasil mengatasi puncak harmonis pertama kehidupan, maka mekanisme bakatnya mampu menampilkan talenta

bekerja. Perasaan (kognitif, moral, atau estetika) terkadang membayangi pemikiran, namun secara umum semua elemen bekerja secara harmonis: perasaan terbuka terhadap dunia, dan pemikiran logis mampu memberi nama dan menemukan ukuran sesuatu dari puncak ini.

Mekanisme kreativitas, yang berkembang secara normal, mencapai keadaan yang memungkinkannya memperoleh hasil tertentu. Dia mulai bekerja. Pada usia ini, mekanisme perasaan sudah mulai maju. Ketika imajinasi dan produk-produknya dievaluasi oleh indra dan pikiran, timbul antagonisme di antara keduanya. Perasaan menang. Kemampuan ini secara bertahap memperoleh kekuatan, dan anak laki-laki itu mulai menggunakannya.

34 tahun- keseimbangan dan harmoni, efektivitas produktif bakat. Harmoni pemikiran, perasaan dan imajinasi, keterampilan psikomotorik, yang diisi kembali dengan potensi energi yang optimal, dan mekanisme secara keseluruhan - lahirlah peluang untuk melakukan pekerjaan yang cemerlang.

55 tahun- seseorang bisa menjadi pencipta. Puncak kehidupan harmonis yang ketiga: pemikiran menundukkan kekuatan perasaan.

Angka Fibonacci mengacu pada tahapan perkembangan manusia. Apakah seseorang akan menempuh jalan ini tanpa henti tergantung pada orang tua dan guru, sistem pendidikan, dan kemudian pada dirinya sendiri dan pada bagaimana seseorang akan belajar dan mengatasi dirinya sendiri.

Dalam perjalanan kehidupan, seseorang menemukan 7 objek hubungan:

Dari ulang tahun hingga 2 tahun - penemuan dunia fisik dan objektif dari lingkungan terdekat.

Dari 2 hingga 3 tahun - penemuan diri: “Aku adalah Diriku Sendiri.”

Dari 3 hingga 5 tahun - pidato, dunia kata-kata yang aktif, harmoni dan sistem "Aku - Kamu".

Dari 5 hingga 8 tahun - penemuan dunia pikiran, perasaan, dan gambaran orang lain - sistem "Aku - Kita".

Dari usia 8 hingga 13 tahun - penemuan dunia tugas dan masalah yang diselesaikan oleh para jenius dan bakat umat manusia - sistem "I - Spiritualitas".

Dari 13 hingga 21 tahun - penemuan kemampuan untuk secara mandiri memecahkan masalah-masalah terkenal, ketika pikiran, perasaan, dan imajinasi mulai bekerja secara aktif, sistem "I - Noosphere" muncul.

Dari usia 21 hingga 34 tahun - penemuan kemampuan untuk menciptakan dunia baru atau bagian-bagiannya - kesadaran akan konsep diri “Akulah Pencipta”.

Jalur kehidupan memiliki struktur spatiotemporal. Ini terdiri dari fase usia dan individu, ditentukan oleh banyak parameter kehidupan. Seseorang sampai batas tertentu menguasai keadaan hidupnya, menjadi pencipta sejarahnya dan pencipta sejarah masyarakat. Namun, sikap hidup yang benar-benar kreatif tidak muncul dengan segera dan bahkan tidak pada setiap orang. Ada hubungan genetik antara fase-fase jalur kehidupan, dan ini menentukan sifat alaminya. Oleh karena itu, pada prinsipnya, perkembangan di masa depan dapat diprediksi berdasarkan pengetahuan tentang fase-fase awalnya.

Angka Fibonacci dalam astronomi

Dari sejarah ilmu astronomi diketahui bahwa I. Titius, seorang astronom Jerman abad ke-18, dengan menggunakan deret Fibonacci, menemukan pola dan keteraturan jarak antar planet di tata surya. Namun ada satu kasus yang tampaknya bertentangan dengan hukum: tidak ada planet antara Mars dan Jupiter. Namun setelah kematian Titius pada awal abad ke-19. pengamatan terkonsentrasi pada bagian langit ini mengarah pada penemuan sabuk asteroid.

Kesimpulan

Selama penelitian, saya menemukan bahwa angka Fibonacci banyak digunakan dalam analisis teknis harga saham. Salah satu cara paling sederhana untuk menggunakan angka Fibonacci dalam praktiknya adalah dengan menentukan interval waktu setelah peristiwa tertentu akan terjadi, misalnya perubahan harga. Analis menghitung sejumlah hari atau minggu Fibonacci (13,21,34,55, dll.) dari kejadian serupa sebelumnya dan membuat perkiraan. Namun hal ini masih terlalu sulit untuk saya pahami. Meskipun Fibonacci adalah ahli matematika terhebat di Abad Pertengahan, satu-satunya monumen Fibonacci adalah patung di depan Menara Miring Pisa dan dua jalan yang menyandang namanya: satu di Pisa dan yang lainnya di Florence. Namun, sehubungan dengan semua yang telah saya lihat dan baca, pertanyaan-pertanyaan yang wajar muncul. Dari mana angka-angka ini berasal? Siapakah arsitek alam semesta yang mencoba menjadikannya ideal? Apa berikutnya? Setelah menemukan jawaban atas satu pertanyaan, Anda akan mendapatkan pertanyaan berikutnya. Jika Anda menyelesaikannya, Anda akan mendapatkan dua yang baru. Setelah Anda menanganinya, tiga lagi akan muncul. Setelah menyelesaikannya juga, Anda akan memiliki lima yang belum terpecahkan. Lalu delapan, tiga belas, dan seterusnya. Jangan lupa bahwa dua tangan memiliki lima jari, dua di antaranya terdiri dari dua ruas, dan delapan dari tiga.

Literatur:

Voloshinov A.V. “Matematika dan Seni”, M., Pendidikan, 1992.

Vorobyov N.N. “Bilangan Fibonacci”, M., Nauka, 1984.

Stakhov A.P. “Kode Da Vinci dan Deret Fibonacci”, format St. Petersburg, 2006

F. Corvalan “Rasio Emas. Bahasa matematika keindahan”, M., De Agostini, 2014.

Maksimenko S.D. "Periode kehidupan yang sensitif dan kode-kodenya."

"Angka Fibonacci". Wikipedia